A Selected Excerpt
Unification of Relativity and Quantum Theory

The neatest trick of modern physics was achieved by Eddington in his unification of relativity and quantum physics. (See Eddington’s Fundamental Theory, pp. 46-47, Cambridge University Press edition.)
According to Eddington, ordinary space is described as a sphere, 4/3 piR³. When we include uncertainty we multiply this by 2pi, a circle or an added circularity. This is equally true at the quantum or at the cosmic level, and is not dependent on size (size is given by the value of R). However, we must also include what Eddington called limitation of scale, a factor of 3/4. I interpret this as meaning that we limit what could be called outgoingness and begin to deal with ingoingness. We then have:
3/4 x 2pi x 4/3piR³ = 2pi²R³
which is the formula for the Einstein-Eddington hypersphere. It is also the formula for the torus with an infinitely small hole, which I have dealt with in The Reflexive Universe.
The torus is a vortex which has two directions of rotation, horizontal and vertical, and is a likely candidate for the “form” of a photon. This is a different subject and beyond the scope of this work, but its relevance to the measure formulae is that it might help when we are ready to go deeper into the nature of the “circle of meaning” which may be a two-dimensional shadow or projection of something more complex.
But how does this insertion of 2pi unify relativity and quantum physics? It does so by equating the curvature of space-time with the curvature of uncertainty. Both the universe and the photon are going through a cycle–very short for the quanta of action exchanged by atoms and molecules, and very long for the universe. Our human time span is about midway between. The curvature of the universe is its closing in on itself, its expansion and contraction, its breathing, its inspiring and expiring. But everything goes through its cycle, the shorter encompassed by the larger, as the day is encompassed by the year. Einstein was unable to unify relativity and quantum theory because he was looking for a “field.” A field is two or more dimensional, whereas the unification contributed by Eddington is at a more fundamental level–that of rotation, or zero dimensionality.
The meaning of uncertainty as a complete circle is that what happens, or is made to happen, within this circle is indeterminate until the circle is complete. Our consciousness is only as large as our lifetime, and can be no shorter (for humans) than, say, the beta rhythm. When we hear a sound less than 16 beats per second, or see a movie less than 16 frames per second, it is not recognized as sound, or as motion.
In other words, we equate a lifetime, no matter on what scale, to the cycle of action. The phases of this cycle, of which the learning cycle is an example, give rise to the varieties of meaning involved in a time period, whether their expression be spontaneous, conscious, active or reactive. Perhaps the key idea is that when by the addition of the 2pi we equate curvature with uncertainty, with freedom, or with the quantum of action, we introduce consciousness and meaning as active principles making the universe take on life. The reversal of expansion which the physicist talks of is not just a collapse of the universe into a black hole, as it is sometimes envisioned, but is its coming to life, a return to the unmanifest with the fruit of what has been gained, an ingathering or harvest. The scythe that cuts down the standing wheat also gathers in the ripened grain.
There are thus two circularities-one spatial, the sphere, and the other the 27T that gives expression to time and, because time is cumulative, to meaning.
The hypersphere, which is the volume of space and time, 2piR³, shows size as R³. Where is time? Space, which can be any size, is the piR³ part (strictly 4/3 piR³, or spherical volume); time is the other 2pi which is not, like space, a measurable extension, but is rather a completion–completion of a life cycle, an era. We speak of the age of the universe, implying a process which has a natural terminus, some kind of life and death. We would never think of space as having a terminus. So it is that there is no T in the formula for the hypersphere. Yet the accepted derivation of this formula involves integration over all time! The complete integration of time, then, makes time disappear, much as when a period of time is over–a day, a year, a century–the time of it has no meaning. Thus time rolls on; day follows day, year follows year. The cycle repeats endlessly.
We are now ready to appreciate the 3/4 that Eddington slipped in. When we go around a circle, 2pi, or 360 degrees, we end where we started. We cannot tell how many days have passed from the clock; we would require another slower clock to count the time of year. The 3/4 must be brought in when we add the extra circularity to the sphere. We must not go all the way around the circle; if we do we will just repeat. Instead we stop at the 3/4 point.
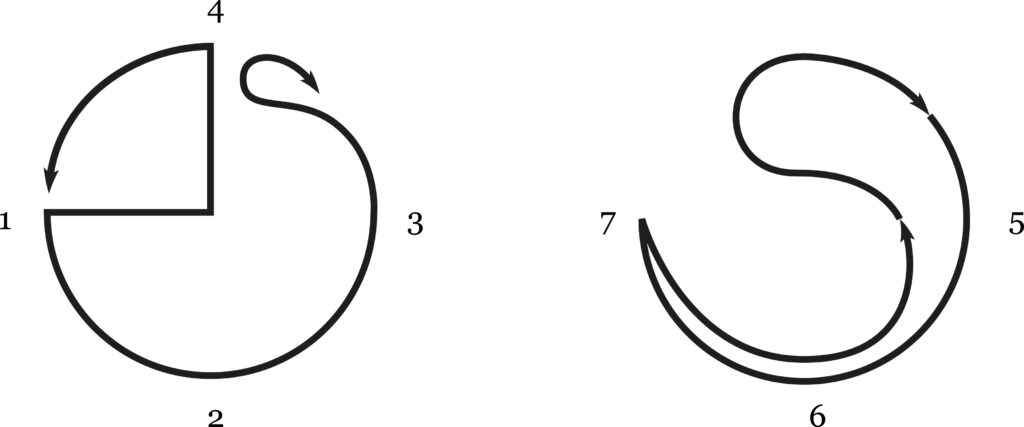
Recall that this is the point in the learning cycle that corresponds to control. If we were to go on to 1 again we would start a new cycle. If we are to stop, or rather if we are not to go past 4, we must turn back, which reverses the direction of rotation and converts the learning cycle to a cycle of application. Admittedly this is conjecture, or is a mere heuristic interpretation of what the hypersphere really is. I do not know; I am groping for an explanation not just of how the universe is, but of why it is. But if we follow the reasoning that explains the learning cycle as four steps taken in one direction and then reversing direction, the reversed cycle will take three more steps–5, 6, 7–to get back to the start. As an example, we learn to play tennis–how to hold the racquet, hit the ball, and so on. Then we play tennis. We have educated our instinctive reaction and action, the two first steps which are unconscious, but which now, due to training and practice, can be depended upon to perform correctly. The steps in the play then start when we see the ball coming (conscious reaction), we move into position (unconscious reaction) and hit the ball (unconscious action).
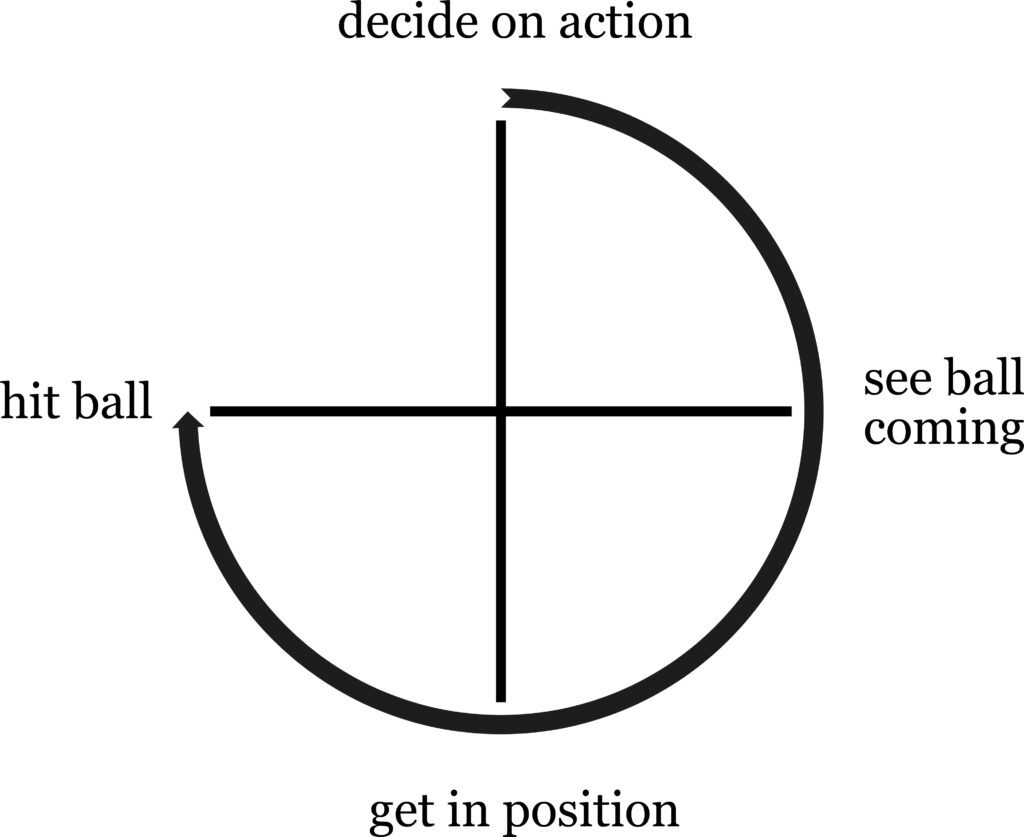
Of course in play we are also learning, and we need this practice continually to remain in top form, but the ultimate goal is to so train our unconscious action that it can be totally trusted.
All other skills have this “anatomy,” involving seven distinct steps, which begin and end with spontaneous action.
Toroidal Space-Time
The so-called coloring problem confirms this sevenness. To color a map on the surface of a sphere requires no more than four colors (the four-color problem); but the torus, which is the shape of the figure whose formula is 2pi²R³, requires seven colors. I asked Eugene Wigner, a prominent physicist, if it was known that the formula for the hypersphere is the same as that for the torus; he answered that it had not been recognized. A mathematician, Chris Clarke, admitted that the formula was the same, but stated that the hypersphere was not the same shape as a torus, though he could not say what the difference was.

Mathematicians generally think of the curvature of space-time as trumpet-shaped (sometimes it is saddle-shaped, but I believe the more sophisticated interpretation is trumpet-shaped). What does this mean? First it means that locally the two curvatures (one for each of the two pi’s) are orthogonal and in opposite directions. But this leaves the ends of the lines unspecified, and I would expect that they must be permitted to extend to infinity.

Such space would extend to infinity both upward and horizontally. Now, if we make a modification as in projective geometry, in which infinity becomes a point, we “close” this open space and still preserve its trumpet shape. That is, we imagine the horizontal part going up and around to meet the vertically extending peak.
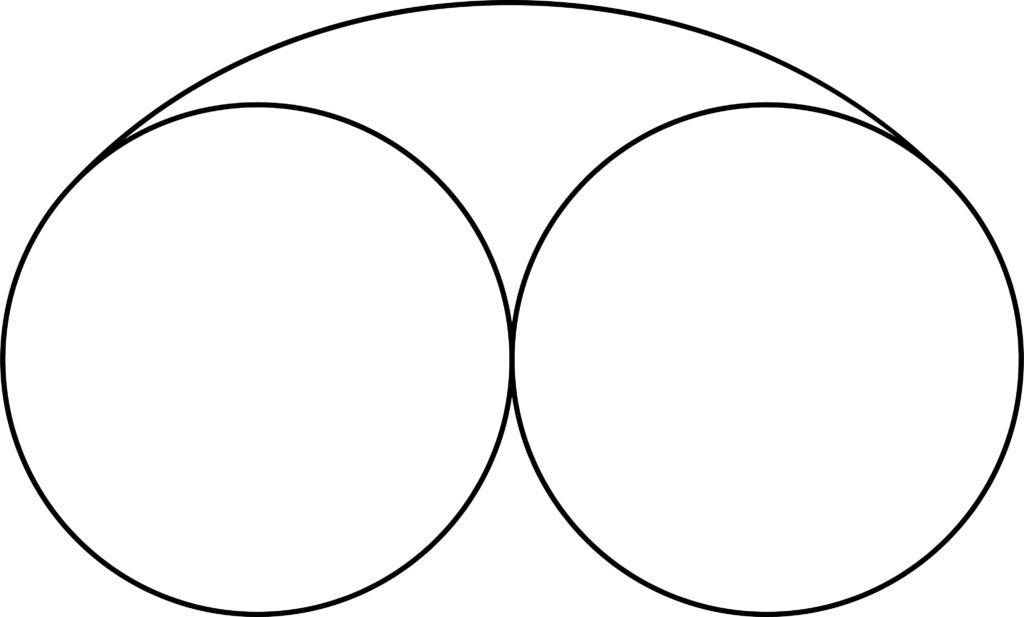
This is not just a rigid grid but a form of motion. It is the vortex, tornado, magnetic field–a form so universal that it is the most natural candidate for a universe.
This exposition regarding the hypersphere may seem a digression from the subject of this essay, which was to show the similarity between the measure formulae and the signs of the zodiac. However, it is justified in that it adds meaning to the circle as a cycle, and supports the correlation of circularity with the cycle of action. Science might dismiss this “anthropomorphic” reference, especially to a cycle as a learning cycle, preferring to say that it is merely another way of measuring. I have a chart before me turned out by a computer. It gives the Julian day (the number of days since 4461 B.C.) as 2417152.92682–a number which may be quite accurate from the measurement point of view, but one singularly barren of significance. And it is not free of a cyclic (anthropomorphic) reference, since it is in “days.” Where was time before there were days? Maybe there wasn’t any.
(c)1987 Anodos Foundation









