A Selected Excerpt
Mathematics and Reality Part I
Dimension

To the mathematician dimensions are variables. Their number does not concern him, and he would be inclined to say that any resemblance to the space and time of the actual world is purely coincidental. I believe, however, that it can be shown that the three-dimensionality of the world of our experience is a result of first principles, a conjecture that might be characterized as ontological-meaning that this conjecture has a certain a priori nature in the sense in which Kant used this term to describe what precedes sense experience. This subject could be said to constitute metaphysics, but it would be a metaphysics that takes into account the findings and implications of science.
An alternative approach would be to show mathematical reasons for a precise number of dimensions. I said it can be shown that there are no more than three spacelike dimensions. Arthur Stanley Eddington said as much in New Pathways in Science (1935) and in Fundamental Theory (1948). In the latter he wrote:
… there cannot be more than three mutually perpendicular rotations connected by circular rotations. “Space,” defined as a domain in which relativity rotations are circular, is accordingly restricted to three dimensions. If we extend this domain to four dimensions, the fourth axis must be connected with the other three by hyperbolic rotations (Lorenz Transformations); in other words, it is a time axis. (pp. 123-4)
While I agree with Eddington that the non-spatial dimensions differ fundamentally from the spatial dimensions, I don’t think it follows, as is often assumed, that they are timelike. Different from space, yes, but to say they are timelike may be misleading. The fact is that the only dimensions that can be dealt with conceptually are space dimensions. If we try to treat time as a dimension we have to objectify it, and this deprives it of its essential character. Time brings surprises; it introduces novelty.
What, then, do we say to relativity, which popular accounts describe as involving time as the fourth dimension? As an in-depth discussion here is not appropriate, I can only reiterate my conviction that relativity’s treatment of time (as a dimension like space) is an error. To suppose that the measurement of time captures its essential contribution would be like assuming that the merit of a novel depended on how long it takes to read.
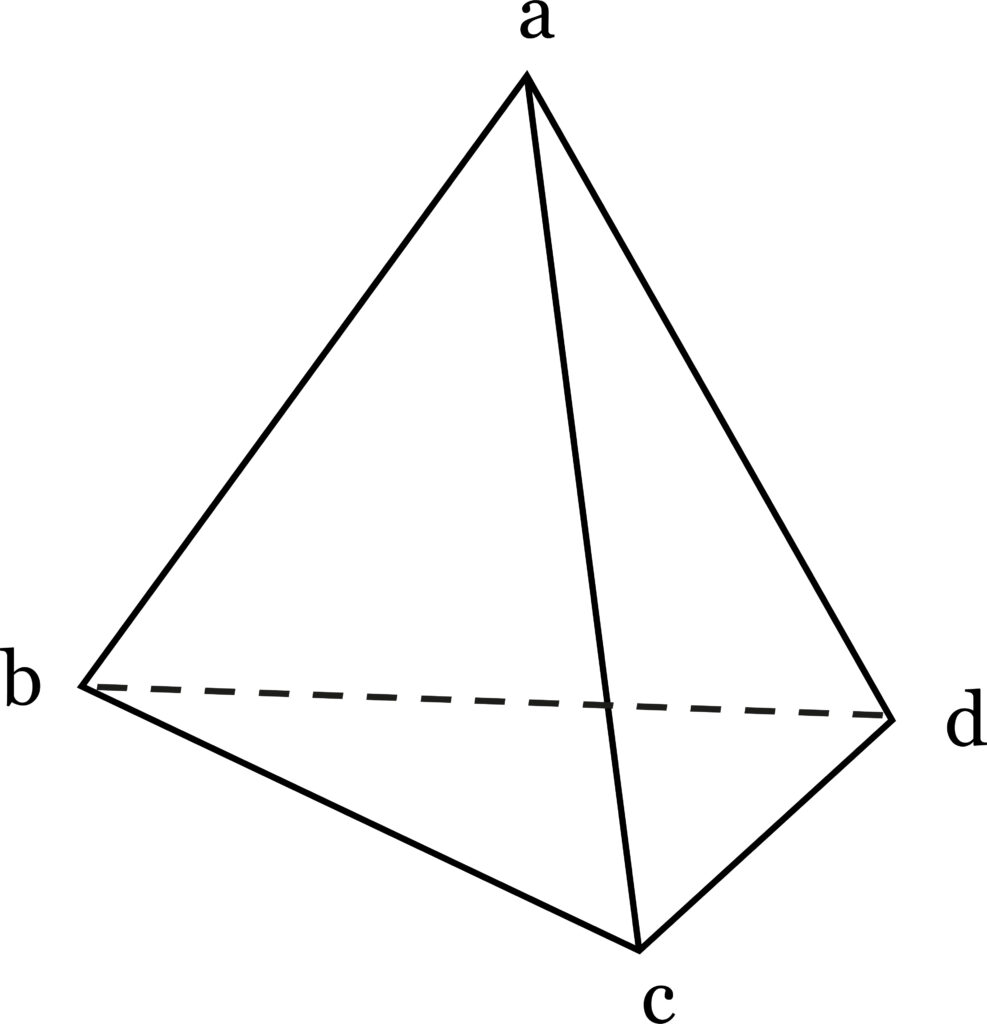
The picture given by science of the world as pure measurement, as a relationship structure with time as one of the parameters, lacks the ingredient that provides for change. But there is an alternative to treating the fourth dimension as time. This is to think of dimensions beyond three as Interior, or internal, dimensions (described in The Reflexive Universe [1976], Appendix 11). The technique is based on the notion that two points determine a line, three points or a triangle determine a plane (two-dimensional space), and four points determine a tetrahedron, which is a volume. If we extend this to five points we get what is called over-determination, or redundancy. Such over-determination would be detrimental in physical structures because it would produce internal stress. On the other hand, if we want to store energy we must use five points. A structure with four points can be connected with four lines equal length:
If we add a fifth point, e, the extra line a – e must be stretched:
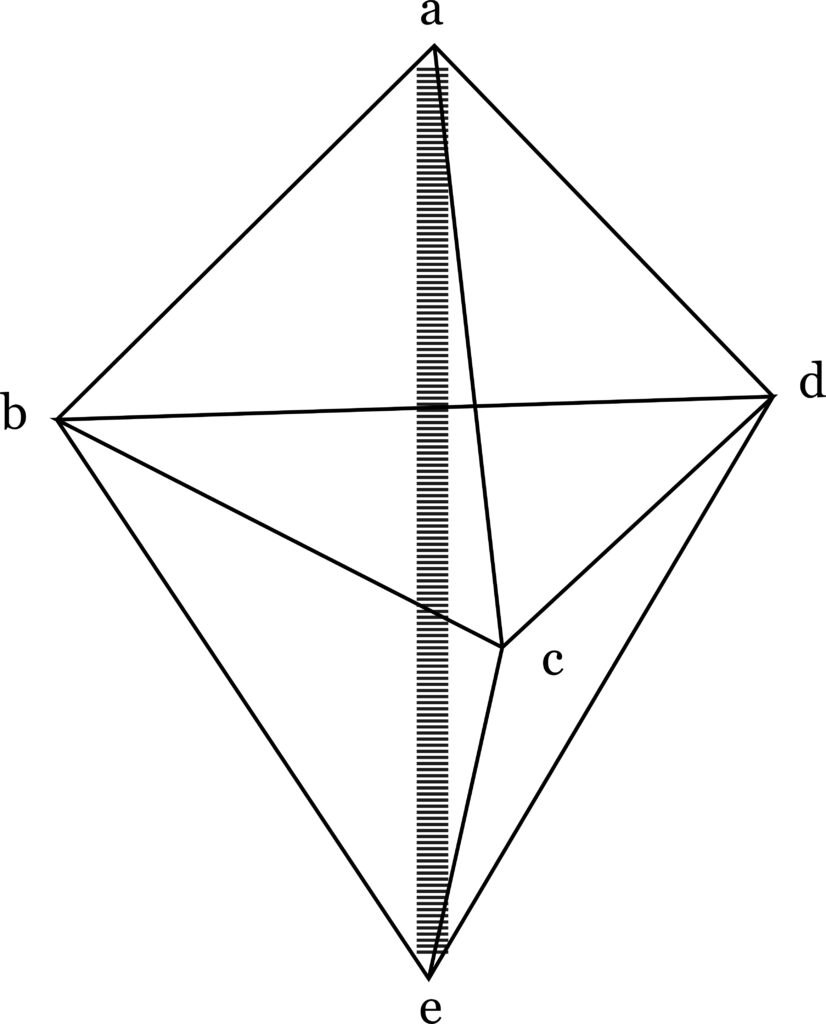
This leads to defining the dimension beyond that of three dimensions as stored energy, which implies reversal of entropy. The energy is stored in the extra internal diagonal made possible with the fifth point (a four dimension).
This technique permits us to talk about still another “dimension”–that involved when we join six points. The resulting figure looks like an octahedron, but has three internal diagonals:
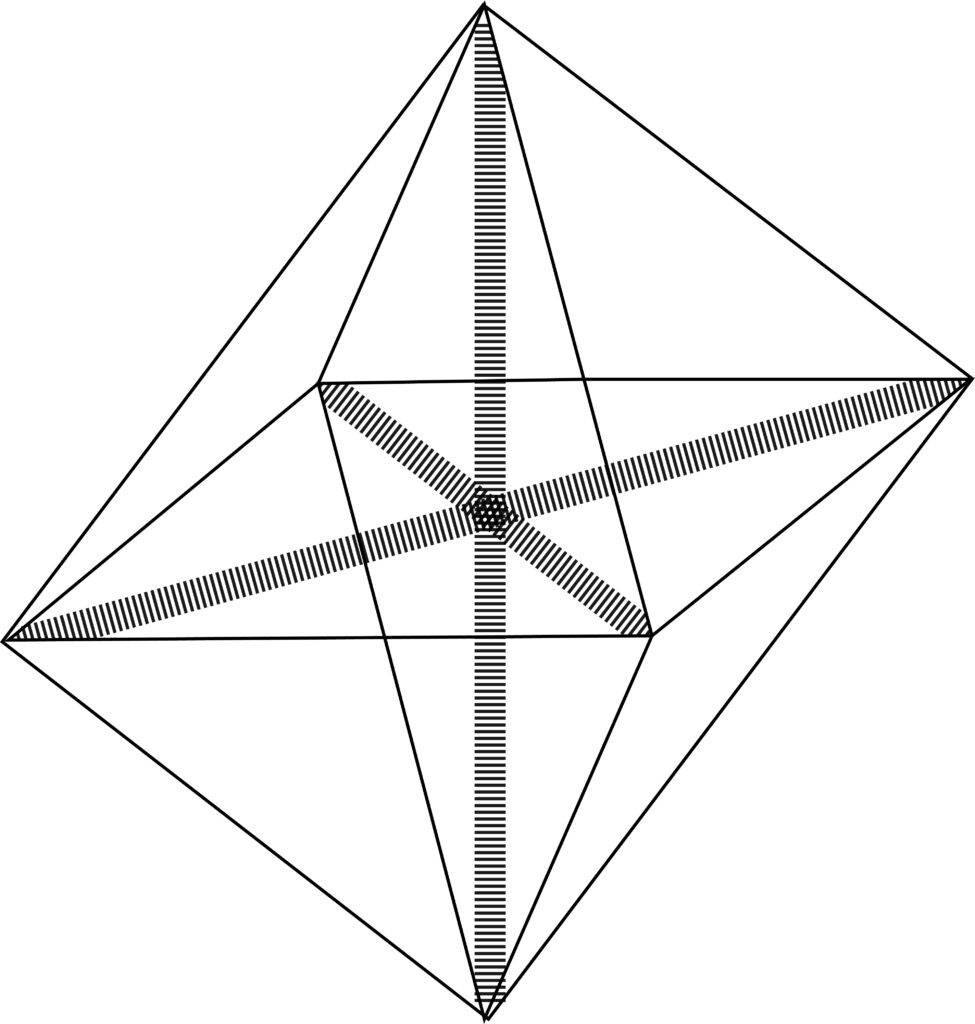
The figure joining seven points has six more diagonals or twenty-one “edges.”
It is not possible to go beyond seven points, for the reason that after seven the subsets can no longer be connected; they divide into two groups. The rules of protective geometry pertain here (see below). Further confirmation comes from the fact that no more than six equilateral triangles can surround a point. We thus arrive by this system at the conclusion that there are three external dimensions (Eddington’s “spacelike” dimensions) and three internal dimensions, and no more. As I will show later, the single point in this system represents zero-dimensionality, or choice of direction. This leads to a seven-fold topology, about which more will be said shortly.
Force
This way of looking at dimension has interesting possibilities. In what follows I will stress that the restriction of mathematics to an exclusively quantitative content is not only unnecessary but prevents mathematics from exercising its potential as a science of first principles. A hint of this appears in physics, where, at the level of fundamental particles, spatial location loses relevance, but force becomes primary.
Now force, as Eddington said, “is a difficult concept.” I would say it is not a concept at all; it is a given that is more basic than space. Eddington equates force with indistinguishability–a rather negative definition, although distinguishability is a possible definition of space. Here we regard force as one-dimensional–it is scalar, one force is either more or less than another–and space as two-dimensional.
The first step in the ontogeny of the universe is from a point to a line. In the physical universe it is pair production–a photon creates a proton and an antiproton, between which there is an enormous force. But this is force between separate things having no interior, whereas the force in the extra diagonal of Figure 2 is internal, or self-contained.
I find it most exciting that this treatment of the first dimension accommodates the substantive aspect of nature, neglected in abstract accounts of the universe as pure geometry or measure. This sounds like a “true” cosmology, for by defining the first dimension as force, we provide for the inclusion of protons and electrons, and hence charge, rather than introducing them as an ad hoc or empirical addendum.
John A. Wheeler, in his Geometrodynamics (1962), attempted to account for charge solely on geometrical principles. He later found this impossible. “Farewell to geometry” was his repeated refrain. Wheeler’s problem was that he was attempting to account for charge with spatial dimensions, attempting to make it objective. Here we are using one-dimensionality, with its inherent asymmetry, to introduce force, and hence charge.
Consider what this means. I have postulated a recognition of the one-dimensionality of force as an intrinsic property of the world of manifestation–a property that is a priorito the world of physical objects. Now, by postulating the fourth dimension as contained force, stored energy or order, we lay the theoretical basis for life, and thus tailor first principles to account for life and evolution.
As I said at the beginning, mathematics is considered to be independent of empirical fact: 2 + 3 = 5, independent of whether the objects counted are apples or votes. But now we have the suggestion that force and the dimensionality of space, usually considered to be empirical facts, can be seen as necessary features of the real world. This poses the question of what kind of science it is that can anticipate characteristics of the world that do not depend on empirical test. Is this mathematics? If not, and we are to continue to insist that mathematics does not tell us how many dimensions there are, or how dimensions are to be interpreted, then we have a new science.
The exegesis of dimension available through thinking of dimension as joining of points, which I have just introduced, is part of set theory, so it could be claimed on this basis that mathematics does deal with the number of possible dimensions.
The same implication of seven-foldedness follows from topology, since the torus, with its connectivity richer than that of the sphere, reflects an equivalent limitation, i.e., that seven points are the most that can be interconnected on the surface of a torus without crossing lines.
This is also shown by the postulates of projective geometry, as given by Veblen and Young in “A Mathematical Science” (1956). In this essay they explain that postulates must meet certain requirements in order to be both necessary and sufficient (for whatever science they are to form the basis). One such requirement is that postulates be independent–that is, each postulate must not be implied by the others. In addition to the six postulates normally given for protective geometry, the authors introduce a seventh: that there may be no more than three elements in a subset.
On my own, I had erected a “science of dimensions” with the help of the figures formed by joining n points as I have described. In this system, three points may not be colinear, four points coplanar, etc. This independence is the same as the independence of postulates discussed by Veblen and Young, and both systems arrive at seven as the number “necessary and sufficient.” (For a more complete exposition, see The Reflexive Universe, Appendix 11.)
Roots
The mind can be slayer of the real. It does so in the sciences just as it formerly did in religion, by setting up idols and mistaking the idol for the reality.
One of these idols is the idea that mathematicians, because “we never know what we are talking about nor whether what we are saying is true, [Russell]” can ignore empirical fact–in other words, that they operate in an ideal world that has no necessary connection with reality. Another idol is the idea that mathematics is the science of quantity. This notion has resulted in the invention of negative numbers to replace subtraction–and subsequently the invention or discovery of imaginary numbers. It is my thesis that this distinction of kinds of number conceals a non-quantitative, or qualitative, factor that, if recognized as such, would require that mathematics acknowledge that it deals in the same distinctions required to describe totality–such as those between mental and physical or between formal and substantial, which are qualitative distinctions of the most basic sort.
The term “imaginary number,” which applies to the square root of a negative quantity, has at times suggested to non-mathematicians that mathematics gives sanction to imagination, or at least to an alternative to the materialist emphasis in science. But this suggestion is strongly resented by mathematicians. They will assure you that complex numbers (numbers that have a real and an imaginary part) are “merely” number pairs. Whitehead actually took time to assure the layman that in mathematics things meant what mathematicians intended them to mean–and quoted Tweedledee to the same effect: “We pay them extra.”
But complex numbers are certainly not just number pairs. They are number pairs in which there is a very special relationship. This relationship, first perceived by Gauss, can be seen as geometric. The imaginaries create an axis at right angles to the real, and together the two kinds of number create a plane:
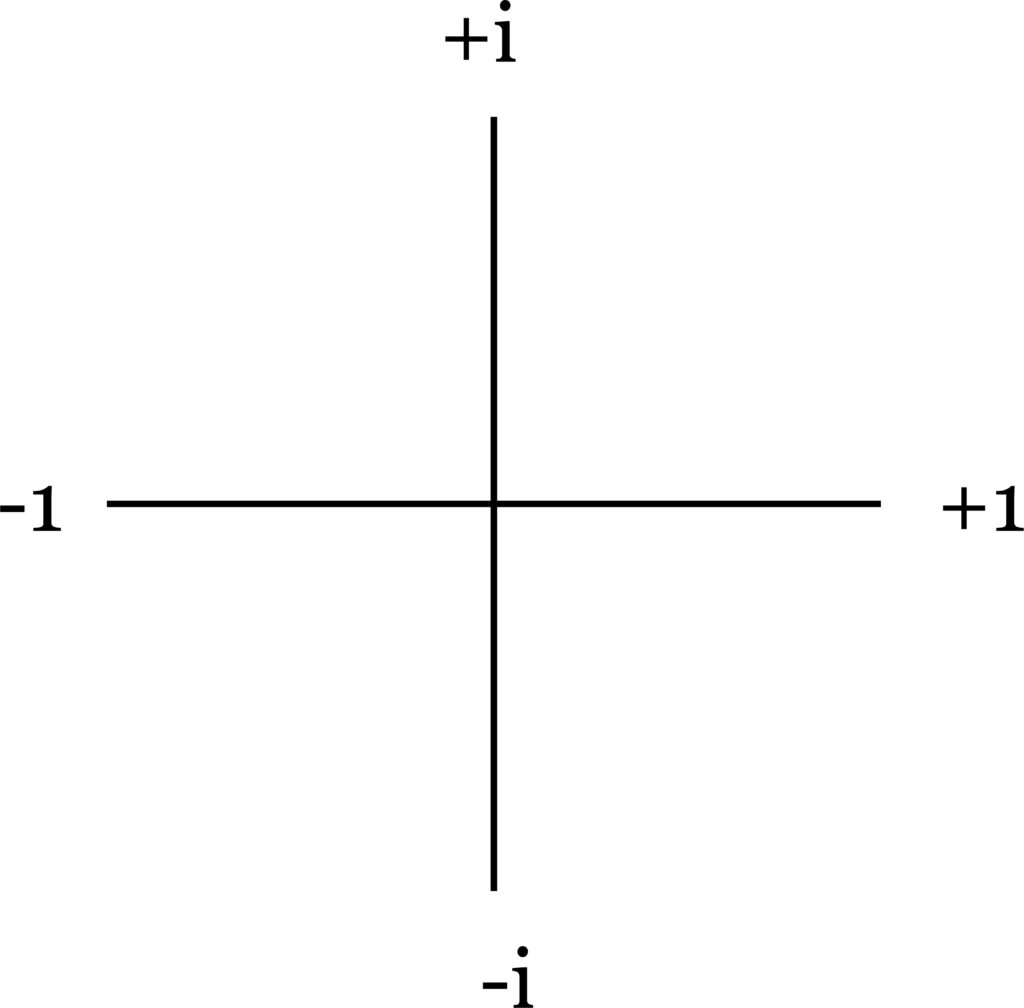
Gauss, who was a geometer as well as a mathematician, devised this expedient to make sense of what had previously seemed incomprehensible – the (represented mathematically as i). In other words, if we think of the minus sign as oppositeness, the square root of oppositeness is halfway to opposite, and if the opposite is 180°, the diameter of a circle, then the square root of oppositeness is 90°, or one-fourth of a circle.
Now the interesting thing is that all roots of unity can be shown on the same circle (the same plane) that displays minus one and its imaginary roots:
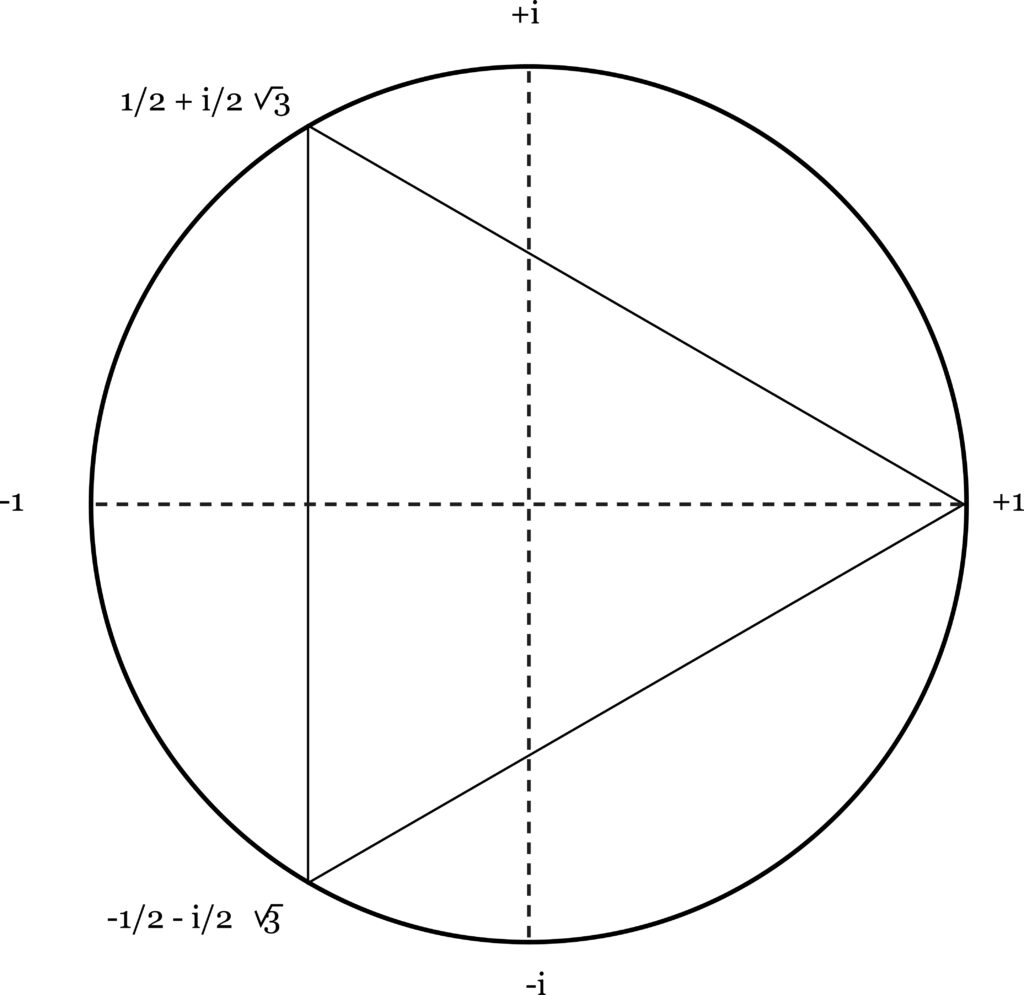
The cube roots of one are the points that divide the circle in three equal parts; the fifth roots of one divide the circle in five parts, etc. But all these roots can be expressed in terms of square roots; that is, located by the two coordinates already established.
Quality and Quantity
To the mathematician this graphic display is merely a technical device, a geometrical illustration of mathematical operation. But what are roots? If we think of unity as a whole and represent it by a circle, then the roots of unity are directions or “signs”–plus one, minus one, and the plus and minus imaginaries–and the circle is the totality of possible directions.
This implies that these four different signs, which indicate different directions on the circle-different aspects are not different in quantity but different in quality. Quantity (absolute value) must be independent of sign.
If we now create another axis through the origin of the previous diagram, an axis perpendicular to the plane of the paper, we can let this axis represent quantity. The circle of aspects we have previously considered represents quality–that is, non-quantitative distinctions of all kinds. An example of three axes used in this way is the color chart found in any paint store:
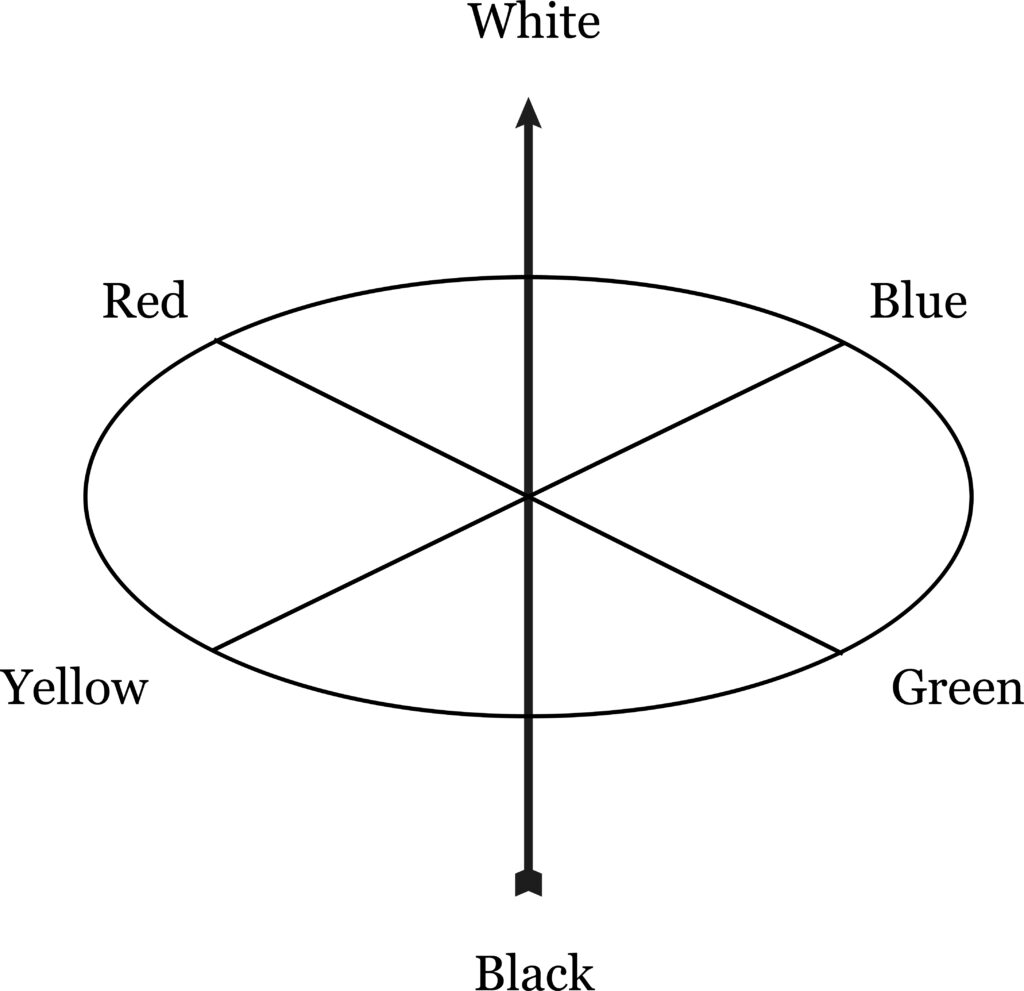
There would seem to be a deep structure in this diagrammatic display of the relation of quantity to quality, which displays quality as a plane with quantity as an axis perpendicular to it. One further con lecture is that just as four colors suffice for a map on a plane or spherical (simply connected) surface, so four distinctions or two dichotomies suffice for qualitative analysis. The problem of the white crow in logic can be handled if we have one other criterion, e.g., crowness defined independently of color. By four distinctions I mean, four categories of distinction (see “Aftermath” p. 91). Thus, facts are distinguished from theories in that facts are particular, theories general. Beliefs are also general but can be distinguished from theories in that they are projective, whereas theories are objective (can be communicated). Of course, facts might differ from other facts in many ways, just as countries can differ in many ways, but mapping does not deal with the character of countries, it purports only to distinguish divisions of a surface.
Another element of this deep structure is rotation. Rotation occurs around one axis and produces variety in a plane perpendicular to this axis. The axis thus has an invariant property in contrast to the variation possible in the plane. Moreover, there can be only two independent axes of rotation in three dimensions.
The formalism presented here provides status for quality as well as quantity in mathematics. Understand that we are not forcing quality into mathematics. Quality is already there in the concept of the negative and imaginary numbers. And note that we now include the “positiveness” of positive numbers as a quality. The signless number (without quality) is different from the positive number. If I have a hundred sheep and one of them is lost, I can say ninety-nine sheep are plus and one is minus, but the number of sheep is still a hundred.
Whether or not this model of the plane of qualification is adopted by mathematicians, it serves to illustrate how mathematics could be enriched by formal inclusion of quality in addition to quantity as within its purview.
It is not difficult to see how the restriction to pure quantity came about. Academic professionalism has to divide the task of science into different disciplines, just as libraries have to classify books according to subject; it would be impossible to do otherwise. (Charles Fort proposed to eliminate the distinction between fiction and nonfiction.)
But when we come to fundamentals–or rather I should say when mathematics or physics or biology comes to fundamentals, as mathematics necessarily does in mathematical philosophy, or as physics does in the study of fundamental particles-the conventions and restrictions that were set up for reasons of expedience have to be dropped. The physicist, whose province was established as restricted to observables, comes at last to the photon, the so-called “particle” of light. Realizing that the photon does not exist except in the act of its detection, he is forced to conclude that photons are “virtual,” which is to say non-observable.
The mathematician, defining mathematics as the science of quantity, finds it necessary to invent negative and imaginary numbers. He is thus led to include just what was excluded in the definition of mathematics.
The origin of dimension
In “The Queen and Mr. Russell” (1980), taking up the question of negative and imaginary numbers, I argued that the plus and minus signsowe their origin to the extraction of roots; thus, as we said, taking the square roots of unity produces plus one and minus one. Of course it could be argued that positive and negative numbers are a convention adopted for convenience, to replace the operation of subtraction with that of adding a negative number. But we are still left with the question of how subtraction enters are subtraction enters mathematics. Is it not an undefined term? It could be said that subtraction is such an operator that minus times minus equals plus, or two negatives make a positive. This makes subtraction equivalent to the extraction of square roots. Moreover, square roots go farther; as I’ve said, the square root of a negative number produces the imaginaries, plus and minus or ± i.
I conclude, therefore, that both positive-negative numbers and positive-negative imaginaries come into being through the extraction of roots of the natural or signless numbers. The latter, I would (with Kronecker) insist are the basic “alphabet” of mathematics. Some years ago I consulted a mathematical text written, as I recall, by my instructor Alonzo Church, which stated that there were negative and non-negative numbers. When I asked Church, “How many legs has a horse?” he became wary and said he would have to count them. I then asked, “How many legs has a quadruped?” He said four. “Were they non-negative legs?” He then admitted the number in this case was without any sign, and that the text he had written was wrong in omitting any reference to signtess (i.e., natural) numbers.
But why this fuss about the origin of numbers with signs? Because if we attend to what is occurring, we will realize that the operation of extracting roots creates dimension. The mathematical purists who maintain that mathematics is “above” any reference to real things such as dimensions, would maintain that dimensions belong to geometry. But now we find, following Gauss, that the mathematical operation of extracting roots creates dimension (see above).
One further point: If we note that the square roots of 1 are ± 1, while the square roots of – 1 are ± i, we can use this difference between plus and minus to establish a basic asymmetry in mathematics that provides for the asymmetry of time.
Time and symmetry
Now the asymmetry of time, especially as manifested in the second law of thermodynamics, has always tormented physicists. This is because what are called the equations of dynamics–those laws that make possible the prediction of planetary motion–do not tell us which way time goes. In fact, to many physicists time is symmetrical, and the second law of thermodynamics, that entropy (the tendency of energy to become more uniformly distributed) always tends to increase, is not theoretical but empirical. De Beauregard, Prigogine, and other physicists devote much attention to this issue, as did Boltzmann in the nineteenth century.
Eddington, too, gave the problem considerable attention in The Nature of the Physical World (1930). He devotes a chapter of this book to becoming, which he links with the asymmetry of time and with entropy. A being from Mars, he says, would be able to read a clock but he would not know from the clock which way time goes. To know this he would require an “entropy clock”-for example a thermometer.
Regarding the connection of causality with the arrow of time, and the scientists who insist that it could go either way, he says:
The crux of the matter is that, although a change described as sorting [of cards] is the exact opposite to a change described as shuffling we cannot imagine a cause of sorting to be the exact opposite of a cause of shuffling… [to do so] would seem equivalent to saying that the activities of matter and mind are related like plus and minus–which is surely nonsense. (p. 93)
While I do not think that the relation of mind to matter can be expressed as simply as plus and minus, I do not feel that the idea is nonsense. In general Eddington says that the world of science is objective and things like color and beauty are subjective. But “entropy is an appreciation of arrangement and organization; it is subjective in the same sense that the constellation Orion is subjective.” (p. 95)
Interesting as he is in his account of becoming, Eddington touches on even more profound questions. He points out that the scientist admits entropy, but not beauty because entropy has a metrical aspect beauty does not possess:
So also entropy is admitted in its numerical aspect; if it has we as faintly suspect some deeper significance touching that which appears in our consciousness as purpose (as opposed to chance), that significance is left outside. (p . 105)
Despite this sensitive appraisal, Eddington does n reach a solution. Yet he comes very close to the conclusion I have reached-that nature does contain just those attributes we call subjective, including becoming and purpose.
The problem of time’s arrow remains an issue because as I said, the basic equations of dynamics do not permit the asymmetry of time. But if we attend to extraction of roots we find a basis for this asymmetry in mathematics.
Note that the equations of motion are quadratic equations, i.e., equations involving x2, and for planetary motion these equations omit linear terms. Such equations are symmetrical because they obliterate the distinction between plus and minus. (If x2 = 4, x = + 2 or – 2.) But these equations do not speak for all reality; they address only that aspect of reality that is symmetrical.
We obtain asymmetry when we use linear equations. And with this asymmetry in mathematics we not only give theoretical status to time’s arrow but we provide a basis for becoming, and for the importance of value, another aspect of things that, like force, cannot be conceptualized. Concept is necessarily objective, two-dimensional; value and force are projective, one-dimensional.
Dirac, in predicting the positron, and hence antimatter, uncovered the basic ontological bifurcation that is only partially suggested by electrical charge. This bifurcation makes possible the reversal of entropy which is to emerge later, in life. It is related to time reversal, symbolized in the Greek myth by Prometheus and Epimetheus.
Of course, we don’t have to trouble mathematics with such subtleties, but in view of the fact that physics is already dealing with not one, but three asymmetries, charge, parity (handedness) and time-the intellectual preference for symmetry should not continue to legislate against the world of becoming.
Here a reference to Henri Bergson is pertinent. Back in 1922 Bergson argued with Einstein against the implication of relativity for the symmetry of time. Time, said Bergson, is continually introducing novelty and hence is not symmetrical. He went further and criticized the concept that time could be thought of as made up of infinitely short instants. Time intervals, said Bergson, can be very short, but they cannot be instantaneous. Now, with quantum theory, it is evident that Bergson was correct. Time can be reduced to intervals of very short duration, but when this is done the energy increases and becomes infinite for infinitely short time intervals. This complementarity, as Heisenberg said, imposes a boundary to smallness in addition to the boundary to bigness that is normally accepted. (We will come back to this later when we discuss infinity.)
The association between energy and time, discovered by Planck, which requires infinite energy for zero time, confirms Bergson’s realization, based on his experience of time, that time cannot be reduced to instants. In this case, we could say that quantum physics, which dictates the relationship h = Energy x Time, is an empirical finding. I will not contest this statement, but will say that the evidence from pair creation that the quantum of action is responsible for the generation of matter, and hence is first cause, should be sufficient to provide it with theoretical status as well.
Mathematics and First Cause
This brings up a most interesting question. Can mathematics deal with first cause? Here I think we discover that there is a higher authority than the queen herself. Up to this point I have argued for the authority of the queen; that is, for the jurisdiction of mathematics in providing deductive principles that prescribe the entities space and time, referred to by Kant as transcendental and a priori. However, in regard to first cause, or the quantum of action, I am ready to confess that mathematics is mute.
First cause is not generally considered to be within the province of mathematics; it is of a still higher order than are other first principles such as space and time. But there are correlates to first cause within mathematics. One such correlate would be a “singularity.” Singularities occur with complex coordinates at a point where the denominator of a fraction vanishes. This renders the function indeterminate and gives to this point a unique status.
Another example of first cause is a prime number. The occurrence of primes, which cannot be predicted and have no antecedents, is the mathematical equivalent of novelty. Yet another case that correlates to first cause is involved in Goedel’s proof of the incompleteness of logic. Goedel demonstrated that any logic that includes the axioms of arithmetic must necessarily involve a proposition that says it is not a proposition. This uncertainty in logic is equivalent to novelty, and hence to first cause.
The difficulty of talking about first cause is to be expected. In fact any procedure that involves indeterminacy violates the ground rules for formalism. Since first cause has to be without antecedents, it cannot be contained in the formalism.
Quadratic and Linear Equations
To return to the subject of dimension, there is an important aspect of this topic to which I have seen no reference in mathematical literature, yet which is taken for granted in measurement. When we use coordinates, in some instances the axes are the same regardless of orientation (isotropic), as in geometry, and in others they describe qualitatively different measures, as in a graph of stock price against time:
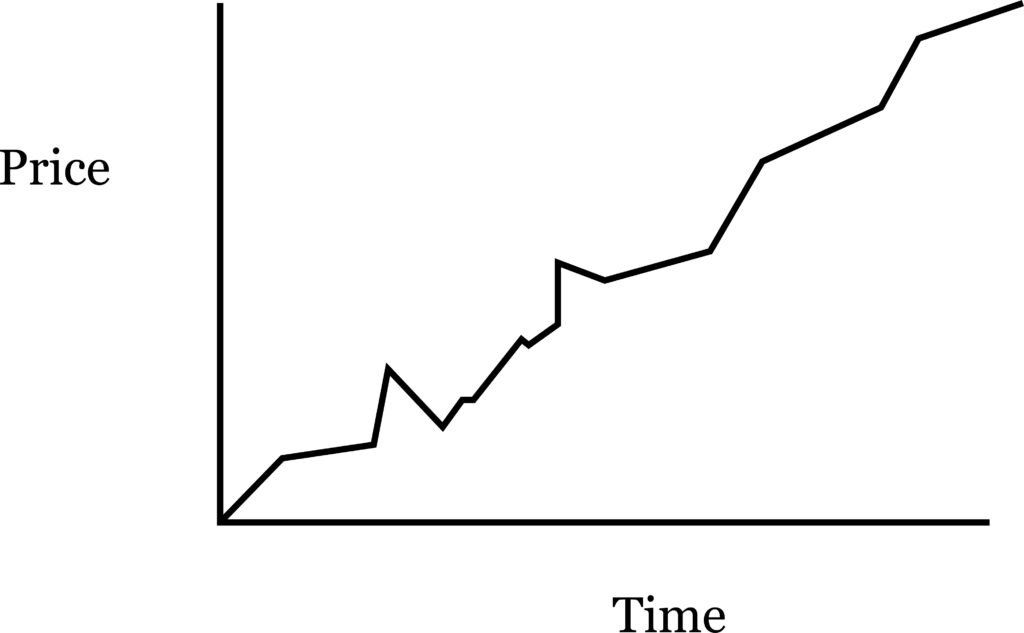
In the figure above, a rotation of coordinates would produce a meaningless picture. The purpose of such a curve is to depict a value (the price of a stock), and value has a nature such that it can only be measured in one dimension. Spatial measures, including length, can only be measured in two dimensions. (We have to have space to separate the ruler from the object measured.)
This difference can be seen as the basis for the distinction between concept and value. An equivalent distinction in mathematics is that between quadratic and linear equations. This is the seed we are looking for-a purely mathematical source for ontological categories.
I stated earlier that quadratic equations eliminated the distinction between positive and negative, and that Dirac discovered the positron by resurrecting this distinction. Again, we could remind physicists who say that quadratic equations indicate a symmetry to time, and who exclude the linear term, which deals with friction, from their equations, that the general case includes the molar world where friction is a factor.
Linear equations have a different function from that of quadratic equations. The difference can be epitomized in that the former preserve the sign and the latter, because they are squares, do not. It is this which makes linear equations asymmetrical and quadratic equations symmetrical.
Years ago, long before I worked out the theory of process, I noticed that the difference between linear and quadratic could serve to express different kinds of human judgment or interaction. First of all there are differences that characterize people and remain unchanged–sex, heritage, age, etc. Second, there are simple judgmental interactions with the environment-expressions of like and dislike, emotional reactions that depend on mood, etc. Such are values and feelings and other projections based on beliefs, prejudices and past experience. The self reacts in terms of its predisposition rather than in consideration of what is outside itself. Such reaction can change over time. Third, we eventually come to make an objective assessment, which is value free. This corresponds to the square or quadratic term.
As we said, the first types of interaction are constants. The second are linear because they involve value and therefore require signs–say, plus for good, minus for bad. The third are value free and hence are objective; they comprise statements about the relations of the object to itself, relations that define the object.
Thus an equation for human perception,
P= k + x + x2
where k are the constants, x is the personal, and x2 the impersonal or objective.
In any case this was an early notion that recognized the essential difference between linear and squared terms.
How does this read on mathematics itself? I am suggesting that the difference between linear and square terms is not merely quantitative, but qualitative, and can be used to describe important distinctions in the real world, distinctions that would be difficult to define in the absence of this formalism. It is the mathematics in this case that provides the important distinction, i.e., contributes meaning to the application. It was my perception of the difference in linear and square terms that suggested the application. Can we, therefore, say that mathematics doesn’t know what it is talking about, when the distinctions of mathematics can so profitably be applied in a variety of situations? We can even say that mathematics, in distinguishing linear from quadratic equations, anticipates the difference between emotion and intellect.
(c)1990 Anodos Foundation
Order Mathematics, Physics and Reality from Amazon $12.95








