A Selected Excerpt
Chapter IV – The Four Levels

In the concept of a fall followed by an ascent, process takes on a shape and becomes something we can describe.
The description begins with the recognition of a purposiveness in process–a goal. To reach the goal, means must be found which to be effective must be predictable, must operate according to law.
Process and Purposiveness
We thus by the single concept of purposiveness, account for a number of apparently different aspects: that process has direction, that it builds on itself, that it must use means, that means must be determinate.
We can now begin to feel a theory taking shape, and as I have noted in the Introduction, if we add that process has seven stages, we have a definite prescription to be filled; we have a set of instructions.
It was at this point that my investigations began in earnest. But before going further, I would like to plead the case for the experimenter with a theory, in order to correct what I believe to be an erroneous concept of how one proceeds with a theory. The usual assumption is that one adopts a theory and goes out to test it, and if it breaks down, one gets a new theory. This might indeed be the case, but, if so, only over a very long period. Most of the time it is just the other way about; when you believe you have a good theory you test it, run into trouble, then you fix the theory. It’s very like a helicopter: the first time you rev it up, it has the shakes, so you study vibration problems until you find a solution. Or like raising a child: he fails his geometry–you don’t get a new child,1 you reinforce the weak point.
Actually, some research programs are operated on the alternative method: if a project is failing, drop the project. But little comes of this except the absorption of funds. Anything that counts is achieved only after much effort both creative and supportive, and I insist that this is the case with theories.
But as applied to cosmology, these observations may seem like generalizing without adequate evidence, for there have not been many overall cosmological theories to judge by. Current theory, with a great show of learning, has moved from naive interpretations of the myth of Genesis to naive interpretations of 19th-century science and has left it at that. There is no comprehensive cosmology based on quantum physics. Almost everyone, within the scientific disciplines, from behaviorists to physicists, is mentally conditioned to think in terms of classical science and fails to appreciate the possibilities offered by quantum physics for a theory which can transcend the limits of classic determinism.
In any case, we now have a theory, or a basis for a theory, and I would like to take the reader through the steps by which I forced out of this theory the reasons for its “structure.” (I put this word in quotes, for I’ve already explained the inadequacy of structure to describe the true development of process.) I use the word structure to denote the relations of symmetry and other properties of what I call the levels through which process descends and subsequently ascends, as we will demonstrate.
Loss of Freedom (an illustration)
In the descent, process loses its freedom in three downward steps. Let us imagine that you are trying to capture a wildcat that has climbed a tree. You lasso him with a rope and make the rope secure. The wildcat can still move about, but he can’t get away. Then you lasso him again and make the second rope fast. The wildcat can still move, but whereas his movement was first confined to a sphere, the pull of the two ropes will constrain it to a circular orbit on a plane. (A circle is the locus of a point equidistant from two given points.) A third rope will complete the process and hold the wildcat in one position.
Similarly, the step down from light to the level of nuclear particles constrains the particle to motion within a sphere (which is the orbit of uncertainty of the electron as described by Heisenberg); the second downward step confines the electron to movement in a circle around the nucleus of the atom; the third to a fixed position of the atom, as in a crystal.
Levels of Descent
The descent is not continuous; it occurs in three steps. But why necessarily three? In the case of the wildcat, it is clearly because there are three dimensions of space. In the case of process, this three-dimensionality carries over into something more abstract, but still threefold. To demonstrate, I would like to present three ways of describing the entities of physics in four stages involving three downward steps. The individual levels will be described in more detail later in the book; here we are concerned only with a method for structuring this concept.
1. Division of initial unity
Described one way, the descent is, as we’ve mentioned (see pp. 18ff.), a division of the initial unity or wholeness in the quantum of action into Energy times Time, and Energy into Length times Force.
2. From homogeneity to heterogeneity
But there is another kind of division. This is the decline from homogeneity to heterogeneity of the entities themselves:
- One kind of photon, which has unit spin2 and no charge.
- Two kinds of nuclear particles, which have half-spin and are charged positively or negatively; i.e. proton and electron.
- One-hundred-odd kinds of atom, with various chemical properties.
- Countless kinds of molecule, with many kinds of properties: mechanical, electrical, chemical, physiological.
3. Change in degrees of certainty
The levels also represent the degrees of certainty which it is possible to have about the entities at the respective stages of process, and these degrees can be correlated to electron volts, a measure of energy.
Level I. The photons at level I are complete in their uncertainty: they are unpredictable. As we have noted, the observation of a photon annihilates it, so that there is nothing left to predict. The energy of a photon that can create a proton is about a billion electron volts, to create an electron about one-half million volts. All photons have total freedom.
Level II. The nuclear particles, electron and proton, created by photons, are the first occurrence of permanent mass and charge, the basic substance of the universe, as compared with the activity of the light that created them. But not all of this activity (or, more correctly, angular momentum) is condensed into mass. For reasons which are still unknown, 1/137 of the angular momentum remains uncommitted, and free. (This 1/137 is known as the fine structure constant.) It is this “freedom” which manifests itself in the uncertainty of position and momentum that characterizes the fundamental particles.
Level III. The atom entails a further reduction, not only in the sense that the charge of the contributing particles is neutralized, but in that the free energy which it radiates or absorbs is drastically reduced to about 10 electron volts (for hydrogen).
Level IV. In the molecule, it is the bonds that have energies, which cover a wide range. We will be interested in the energies of approximately 1/25 of an electron volt, which is that of the average molecule at room temperature. Why? Because according to our theory, it is at this energy level that life becomes possible.
This last energy level, it would appear, is the working base that process has to reach before it can start building up again. By this, we mean building the complex organic molecules such as proteins and DNA that are the basis of life, which requires a temperature between O and 45 degrees centigrade.
Necessity for Free Will
The reader may perhaps be familiar with current ideas of how life arose from electrical discharges in the early atmosphere of methane. Such discharge has been experimentally tested and found to produce minute amounts of many of the amino acids necessary to life. This may indeed have been an important step in the creation of life, but in our view it could by no means have been sufficient. Our position is that life requires, in addition to materials and conditions, an act of will comparable to the purposiveness of the quantum of action. I am afraid this will seem unscientific, but I hope to show the contrary: that the hypothesis I am setting forth requires a minimum of assumptions. And it does not hide the problem under the rug, as do current interpretation of the Darwinian theory.
Neither of the preceding ways of distinguishing the levels lends itself in any clear-cut fashion to the higher kingdoms, plants, animals (man). (I am putting man in parentheses to indicate that he is not to be thought of as the sole representative of the seventh kingdom. In fact, part of the job is to arrive at a definition of the seventh kingdom, or at least a description that will distinguish it categorically from the others. It is not enough to make man a “naked ape” or “an ape with a club” or even an animal that “communicates through language” or “is capable of abstract thought.” We have in the theory a tool that provides for more basic distinctions, and we should use it. This is what the levels provide. And it is perhaps not too early to point out that what is emerging is a scheme of the cosmos in which life, far from being “a green scum on a minor planet,” as one scientist put it, is inherent in several levels of organization that are intrinsic to cosmology. The seventh kingdom, which includes man, is one of these levels of organization.)
So how can we show that the higher kingdoms are categorically distinct and occur on separate levels?
Symmetry of Descent and Ascent
There are several possibilities, but the one that is clearest, because it is visual, draws on the well-known, though neglected, symmetries of minerals, plants, and animals. This was first brought to my attention by Fritz Kunz, who discussed the subject in his article “On the Symmetry Principle.”3
While D’Arcy Thompson in Growth and Form4 devotes a large part of his thousand-page work to the subject of symmetry, he does not appear to notice the eloquently simple fact that the kingdoms may be distinguished by symmetry.
Molecules–level IV, stage four:
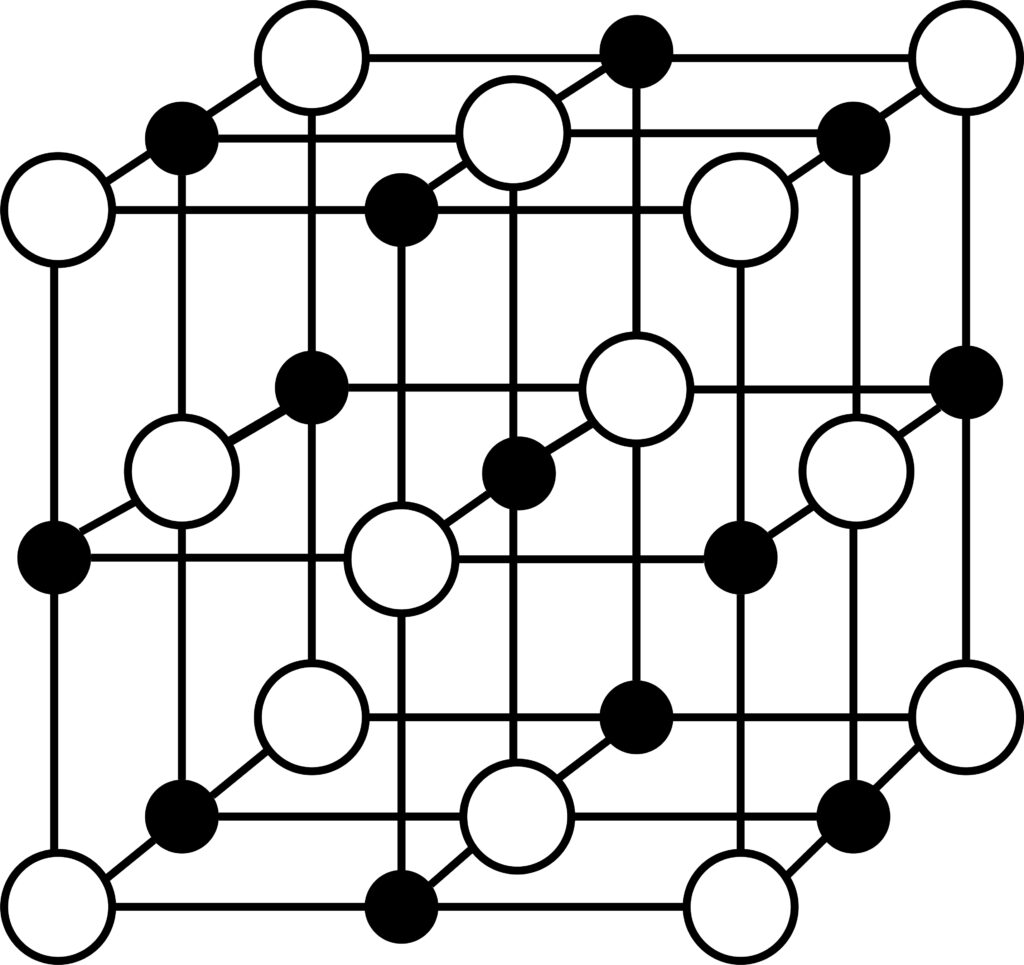 |  |
Crystals, in the molecular kingdom, have what is known as complete symmetry: they comprise molecules in rows, columns, and layers monotonously and indefinitely repeated; three axes of symmetry and no freedom. By the term “axis,” I mean a direction of symmetry.
It seems beyond comprehension how a virus molecule, having a molecular weight in the millions, can be marshaled into the strict order of a crystal, yet this is true. All molecules can occur as crystals.
Plants–level III, stage five:
 |  |
Plants exhibit their one degree of freedom by growing vertically. The top of the plant differs from the roots, but right and left are similar, front and back are similar. This is known as radial or cylindrical symmetry; two axes of symmetry.
Animals–level II, stage 6:
 |  |
Animals differ front and rear, and also top and bottom, but are similar right and left. This is bilateral symmetry; one axis of symmetry.
Note that the greatest symmetry (three axes) occurs with molecules, the least with animals, suggesting a correlation of symmetry with constraint. We have here a simple way to make a quantitative distinction among these three kingdoms by counting the axes of symmetry, or conversely the degrees of freedom. We may say of crystals that they have no freedom, while plants have one degree of freedom (their ability to grow) and animals two degrees of freedom (their ability to move about two-dimensionally on the surface of the earth). The flight of birds is also two-dimensional in the present sense, since birds steer vertically or horizontally.
But there is a position open for a kingdom with three degrees of freedom and no symmetry. (Kunz indicates a tendency toward asymmetry in the human face. There is also left- and right-handedness and the recently discovered fact that the two sides of the human brain have different functions. As already mentioned, however, the seventh kingdom is not to be thought of as limited to humans.)
The question now arises: can a similar quantitative distinction be applied to the left-hand side of the arc–to atoms, to nuclear particles, and to light?
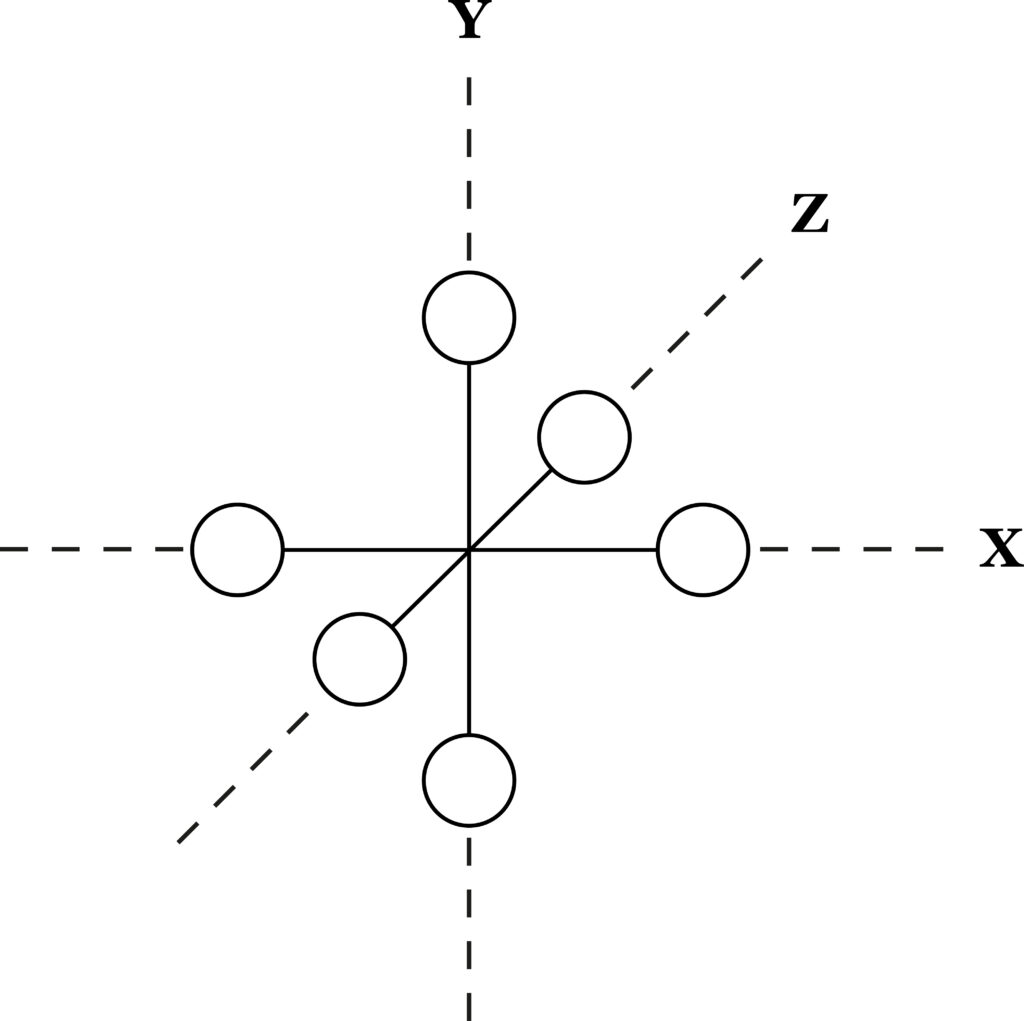
Atoms. level III, stage three
While the image of electrons traveling around a central nucleus like planets around a sun has been supplemented by more abstruse models, the radial symmetry of the atom still holds, as is brought out by its magnetic properties.
What gives the atom one degree of freedom (like the plant) is the fact that it can absorb or release energy without any prompting from outside. Its energy state is unpredictable (or free). The same can be said of plants, since growth correlates with energy storage by carbohydrates, etc.
Nuclear particles. level II, stage two
Let me first take up freedom. Recall Heisenberg’s observation that we are uncertain of the position and momentum of the nuclear particle: hence it has two “degrees” of freedom. The product of the uncertainty of position and momentum is a unit of action and may not be less than the value h. The formula for this is L x ML/T = ML2/T = h. This situation is similar to that of an animal at large: we can know only an area (L2) in which the animal (M) would be after a given time (1/T). The product cannot be less than a given value, ML2/T = h.
As to the symmetry, this question cannot be answered with finality, but the experiments proposed by Lee and Yang, and completed by Mme. Wu, which discovered that chirality, or handedness, characterizes nuclear particle reactions, suggest this possibility, for only that which has bilateral symmetry can have handedness. (One could not have a right-handed circle or cone, but one can have a right-handed thread or spiral.)

Light: level I, stage one
To carry out the scheme, we should show that light has no symmetry and complete freedom. I can’t see how to establish its asymmetry5. Light is certainly the most completely free form of existence there is: a photon released at a certain point could be anywhere within a radius of 186,000 miles a second later. In addition, we can again point out that since observation annihilates the photon, it cannot be predicted.
As for the seventh kingdom, we will make lack of symmetry and complete freedom a definition of the kingdom. Since this is the highest form of existence, we cannot expect to define it anyway, and this, while a negative definition, is as good as we can expect.
We may put this all together in a chart:
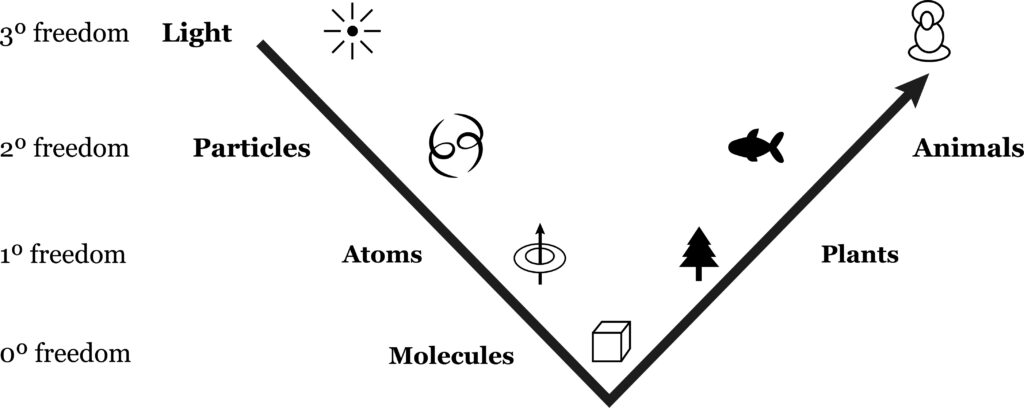
Anticipating the Character of the Kingdoms
Now let us take advantage of this charting. Notice that there is a considerable economy of definition. The “degrees of freedom” describe the levels applied to kingdoms at the same level on both the right and the left side of the arc. And we can extend the correspondences further. Thus it would be expected of the atom that its position can be determined, as can that of plants. This is the case: the atom can be fixed in a crystal. The nuclear particle, unlike the atom, should have a fixed (internal) energy. This is the case: the energy fixed in the mass of the proton or electron is quite exact (known to the fifth decimal point). Correspondingly, the animal, once grown to maturity, retains a fixed weight in a way that is not true of the plant, which continues to grow.
A further point: animals and plants interchange position and energy in respect to which is free and which is constrained. Thus the animal is free to move but unable to create its own energy, while the plant is fixed in position but able to synthesize energy from sunlight.
Likewise, nuclear particles are free to move in the sense that their position cannot be determined. But their mass is fixed, while the atom, which can be fixed in a crystal, is able to absorb or radiate energy.
As we have noted, motion requires two degrees of freedom, while energy absorption requires one degree of freedom. Of course, it was the descent or “fall” into constraint followed by an ascent that was our basis for the arc. The inclusion of degrees of freedom adds precision to this conception by providing a quantitative measure.
We can now recognize that the kind of determinism which the behaviorist talks about has quite a different meaning from that of the physicist. Thus, to say that an animal is attracted by food or conditioned by drives in the sense that a weight is attracted by gravity is quite erroneous. The animal may be attracted to the water hole because of thirst, but it isn’t going to move in accord with an exact “law” as would a freely falling weight, subject to a force proportional to the inverse square of the distance. A drive, such as hunger, does not wholly determine animal behavior as law determines the behavior of an inert object.
The Reflexive Universe
We have discussed similarities between the left and right sides of the arc. What is the difference between the two?
Notice again that the entities of exact science are on the left. Life, on the right, is not accounted for by science.6 The higher kingdoms on the right have acquired an ability not present in those on the left–an ability we describe as voluntary, as distinct from random. Thus the movement of animals is voluntary, whereas that of nuclear particles is random; the storage and release of energy of plants is voluntary, whereas that of atoms is random.
This distinction, obvious to common sense, is difficult to maintain in the framework of current science because there is at present no formal expression for control. Such an expression can, however, be developed with the tools available from science.
Formal Expression for Control: Position and its Three Derivatives
Science depends on providing formulations for describing otherwise elusive concepts. Recall the paradox of Zeno which pictured a race in which Achilles was to overtake the tortoise, who had a head start. Achilles could never pass the tortoise since he would first have to get to where the tortoise was, by which time the tortoise would have moved on, and so on. Silly, but without a formal expression for velocity, which would permit a comparison of rates rather than of positions, the problem remained baffling.
Newton provided the necessary formal expression in the calculus, where he defined velocity as the rate of change of position with respect to time, and acceleration as the rate of change of velocity with respect to time.
Velocity is known as the first derivative (of position), acceleration as the second derivative. These two expressions laid the basis for the theory of gravitation.
While Newton mentioned a third derivative, he made no attempt to give it a physical meaning. What is it? Since each derivative is the rate of change of the quantity derived (i.e., velocity is the rate of change of position, acceleration the rate of change of velocity), we may conclude that the third derivative is the rate of change of acceleration.
Every automobile driver has direct experience with the third derivative, for in controlling the car by pushing the accelerator, applying the brake, or changing its direction with the steering wheel, he is changing its acceleration. This, in fact, is control. So we can say, just as acceleration is change of velocity, so control is change of acceleration and is the third derivative, and hence has status.
The neglect of the third derivative by classical physics is traceable to the fact that it cannot be used for prediction. We may, of course, as in a guided missile, lock the controls to home in on a target and hence render control determinate, and this is the special case covered by cybernetics. But in the general case, we must go a step further and recognize that control is “outside the system.” It is indeterminate–the driver is free to steer the car where he wishes. This does not deny its existence as a factor in evolution.
We can diagramatically represent the derivatives by a circle on which position is shown at the right and its three derivatives in sequence clockwise.
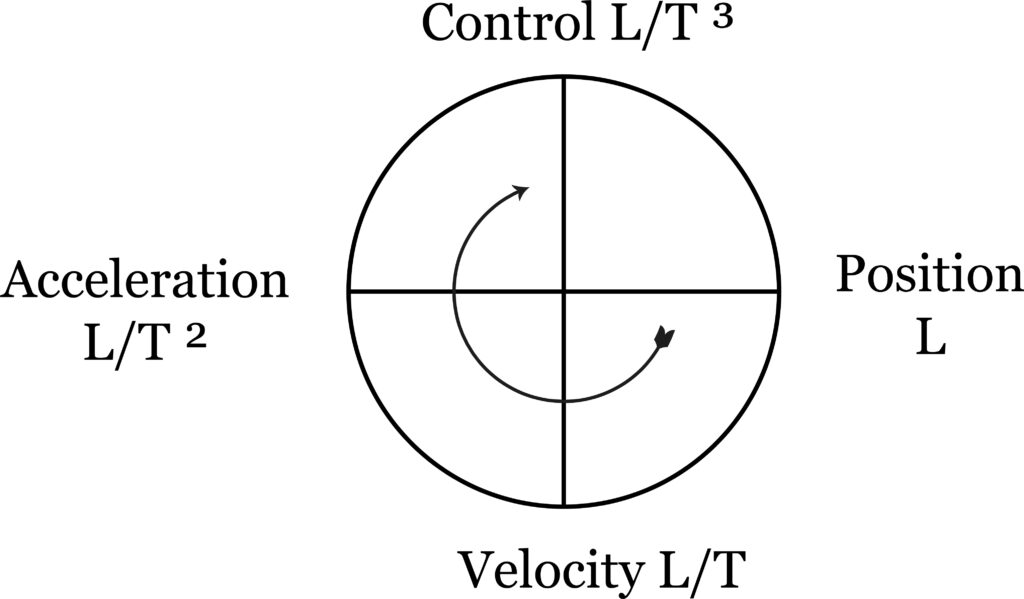
Such a circle is also representative of the cycle of action, and applies to any repeating cycle, such as the swing of a pendulum.
Here, however, we are interested in the fact that the representation implies that derivation returns to itself after four applications. Is this the case? Does the fourth derivative reduce to a position? Yes.
For example, when you’re driving a car, your control of the car is governed by position, for that is what your destination is, a position in space. Or again, the control of a guided missile is directed by the position of the target. Therefore, the fourth derivative is position. In other words, if we divide by T four times, we are back at the start: 1/T4 = 360 degrees = O degrees. (Standing still, known as the identity operator in science.)
We propose to make control a criterion for the description of entities on the right-hand side of the arc (see p. 41 ). Our right to do this stems from the fact that control can be identified with the third derivative and is therefore equal in status with other derivatives (velocity and acceleration). Or, again, control is evident to observation: an automobile, a paramecium, a flying saucer can be observed to be under control or not under control. And control is evidence of life.7
Footnotes
1 Newton flunked his mathematics.
2 Spin is an additional property of particles.
3 Kunz, Fritz 1. “On the Symmetry Principle.” Main Currents in Modern Thought, vol. 22, no. 4 (March-April 1966).
4 Thompson, D’Arcy W. On Growth and Form. London: Cambridge University Press, 1917, 1963.
5 We might point out that symmetry requires measure, and light is before measure.
6 Biology, the “science” of life, is solely descriptive. It does not explain the life force, why things are alive, or why they move.
7 I have recently learned (January, 1971 ), thanks to an interesting volume by Marjorie Grene entitled Approaches to a Philosophical Biology (New York: Basic Books, 1968) of the ideas of a German biologist, Helmuth Plessner. Plessner’s concepts stem from the recognition of the way in which an organism bounds itself, its “self-limitation,” which Grene translates as “positionality.” Not only is this quite similar to what I call “control,” but it leads Plessner to postulate three levels of “positionality”: vegetation, animals, and humans.









