by Arthur M. Young
Are there two worlds, an ideal world of mathematical relationship and a “real” world of actual objects? A consideration of dimensions, which link the two worlds, brings the question into focus.
Outwardly there are reasons to believe in the duality. Not only is it possible mathematically to construct spaces which may have any number of dimensions, and thus differ from the space of the physical universe with its three-dimensionality, but we may in mathematics have “imaginary” dimensions-a designation which, at least at first glance, indicates an unreality, or a reality of a different order than we encounter in the measurement of actual space.
The duality is further supported by the general trend toward specialization in scientific disciplines. This encourages the invention of mathematical fictions for their own sake and without regard to practical application; and, while what was thought to be a pure abstraction has often turned out to have practical application, there is always a feeling that if the criterion of usefulness were made the sole justification for mathematics, creativity would suffer. The finest blossoms would be mowed down, and the garden of the queen of the sciences reduced to supplying the kitchen with “useful” vegetables.
But here we must reckon with another consideration. Mathematics, even of the purest sort, is fostered and even inspired by the necessity of having to deal with the physical world. In fact, the birth of probability theory is credited to a gambler who engaged Fermat to work out the odds in his gaming activities. Again, we have the more recent example of the theory of relativity, which, prodded by the negative results of the Michelson-Morley experiment, and the practical impossibility of synchronized clocks for separated observers, established categorical implications about measurement. Some of the advocates of pure mathematics would claim this was only a “reality condition,” leading one to select from the larder of pure mathematics but one of many possibilities, but for the present inquiry, this claim begs the question, since it is the nature of measure that is under scrutiny.
We come back, therefore, to the question, “what is dimension?” Perhaps the most general definition is that it is the range of a parameter-that is, of a variable which can take on different values. Under this definition it is possible to have any number of dimensions. But when we use dimension in the more limited sense of its applicability to a universe, particularly to measurement in space, we are faced with certain facts about reality, or real space. It has three dimensions, not four or five, and, even if we call time another dimension, or assign dimension to rotation, we do not efface the obvious and sensible character of length, breadth, and height, and their intrinsic difference from time and rotation.
There are a number of ways in which the concept of dimension, as we are forced to employ it in dealing with the physical world, takes on a character that it does not appear to inherit from the realm of mathematics. The difference between time and space, the difference between position and rotation, and, indeed, the very notion of a world of precisely three dimensions, seem foreign to the mathematical mode of thought, to which the nature and number of dimensions is considered arbitrary.
We will endeavor to show that this view is actually not even valid within mathematics itself, but before we can do so, we must first examine the concept of dimension as it applies to measurement of the so-called physical universe.
Cartesian vs. Spherical Coordinates
Ordinarily we think of space as measured by rectangular or Cartesian coordinates. This custom seems so completely natural that it goes unchallenged (fig. 26).
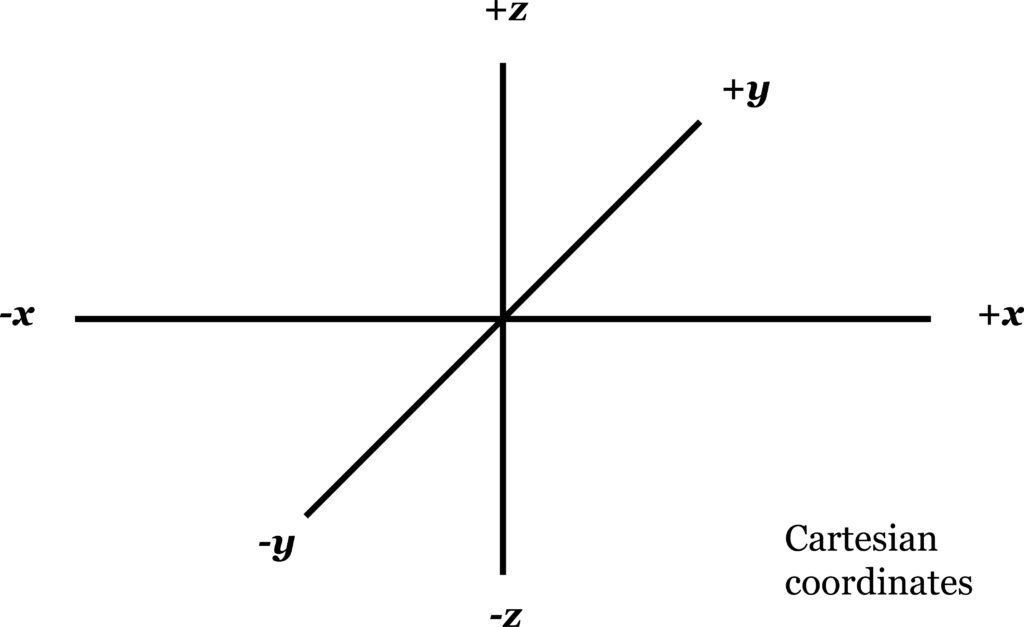
Cartesian coordinates are thought of as extending in three mutually perpendicular directions from an arbitrarily chosen origin, 0: an x coordinate extending from left to right, a y coordinate perpendicular to the plane of the paper (shown below at an oblique angle) and a z coordinate extending up and down. Such coordinates are understood to extend indefinitely in all directions. With them, one can describe the proportions of a house, for example.
Conventional and natural as is this coordinate system invented by Descartes, there are two important respects in which it is deficient, and has led to a false notion of reality.
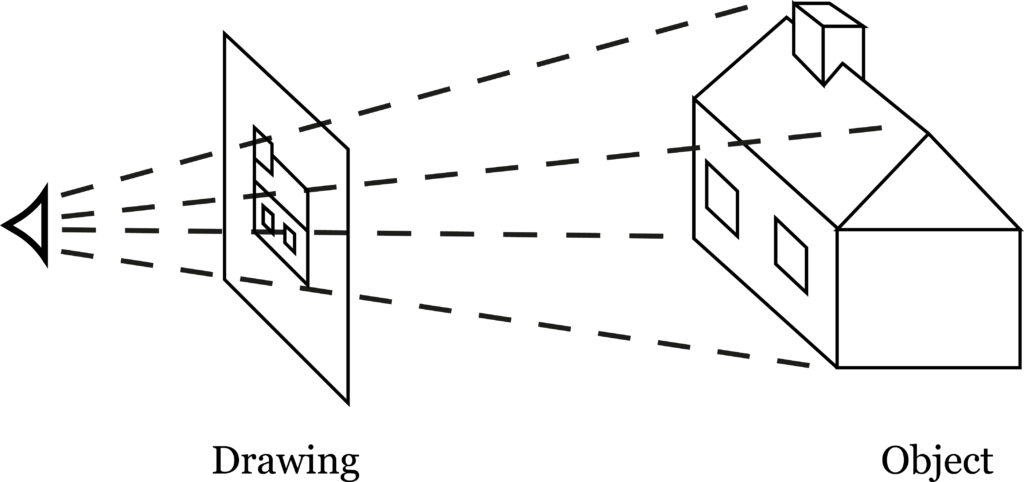
The first deficiency is that it provides us with no notion of scale, or the size of the object. While scale may be indicated on a drawing as so many feet to the inch, this only begs the question, since the feet which the inch represents are in a different logical category, as it were, from the measurements on the paper; they require experience for their proper appreciation. One must know what a foot is, and this knowledge is of a different order to that involved in the drawing. We may come to an appreciation of this if we think of the drawing as though it were on a transparent sheet placed in the line of view and coinciding with the outline of the actual object drawn (see fig. 28). The scale of the drawing is equivalent to the ratio of the distance of the drawing from the observer (or point of observation) to the distance of the actual object depicted. But to know what this means, the observer must operate in real space with the actual distances involved. He must experience the unit distance by some flesh and blood action, such as pacing the distance off, or perhaps even living in the house. The size of the door must be such that he can walk through it.
The second deficiency is that rectangular or Cartesian coordinates give no account of orientation. In ordinary engineering practice, or when we hang paintings on a wall, this occasions no difficulty. Gravity is always present, and we hang our pictures “right side up” and set up buildings with the floor down and the roof above it. The mason uses his plumb bob and level as much as his trowel and mortar board.
But it is not always so simple. In using a map it is very important to know how to orient the map with respect to north. In surveying, it is just as important to record the angles of the boundaries with respect to north as it is to measure their length. In the assembly of a machine we always require not just the drawing of the parts, but the general layout, a larger drawing that shows how the parts are put together, how they are oriented with respect to the whole. Otherwise the carburetor may be installed upside down, or the controls rigged backwards.
How do we show orientation on a map, or on a drawing? The drawing in Cartesian coordinates takes care of this by the convention that its bottom edge is intended to be parallel with the earth’s surface. Similarly, the map carries an arrow to be brought into coincidence with a compass needle, or it shows parallels of longitude and latitude which ultimately refer to the earth’s axis.
But such references-like that of indicating scale as so many feet to the inch-leave the crucial question of orientation to be resolved by methods outside the system. The coordinates of the map or drawing are incomplete. They omit or bypass the necessity of an observer of the map or drawing who will have the task of correctly orienting it.
Spherical Coordinates
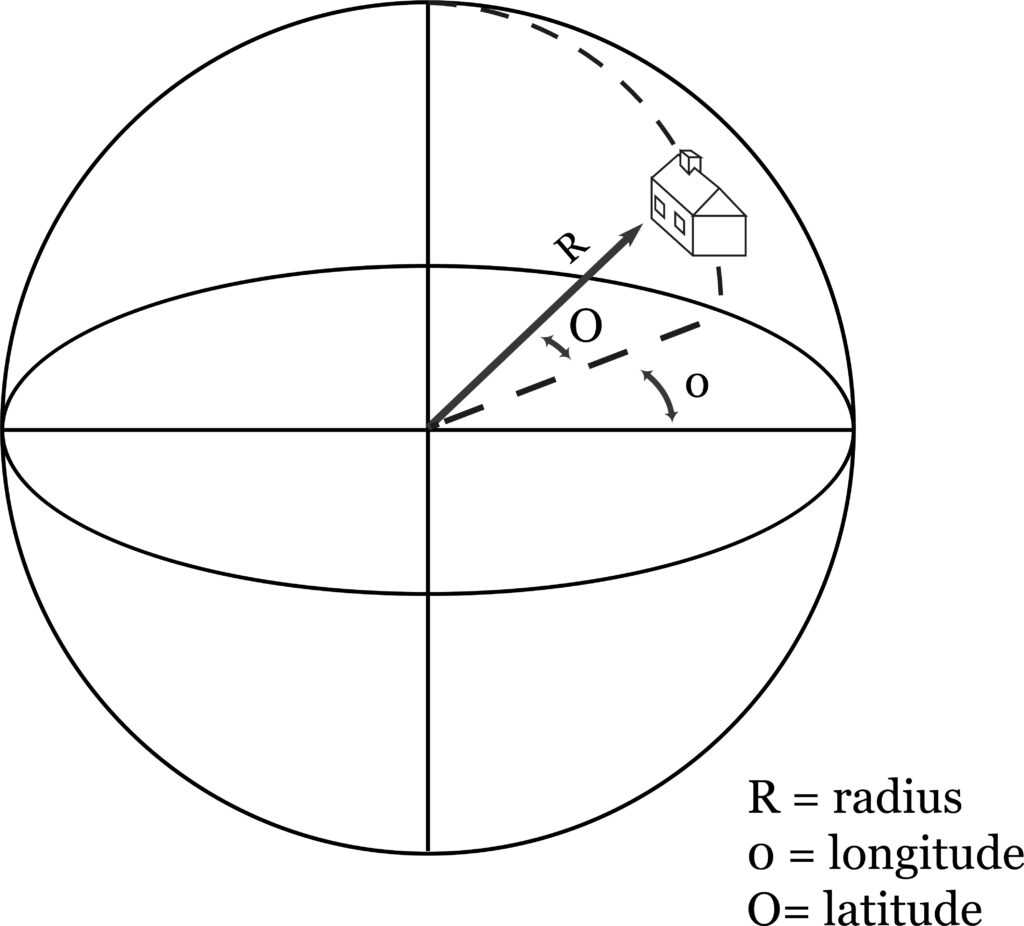
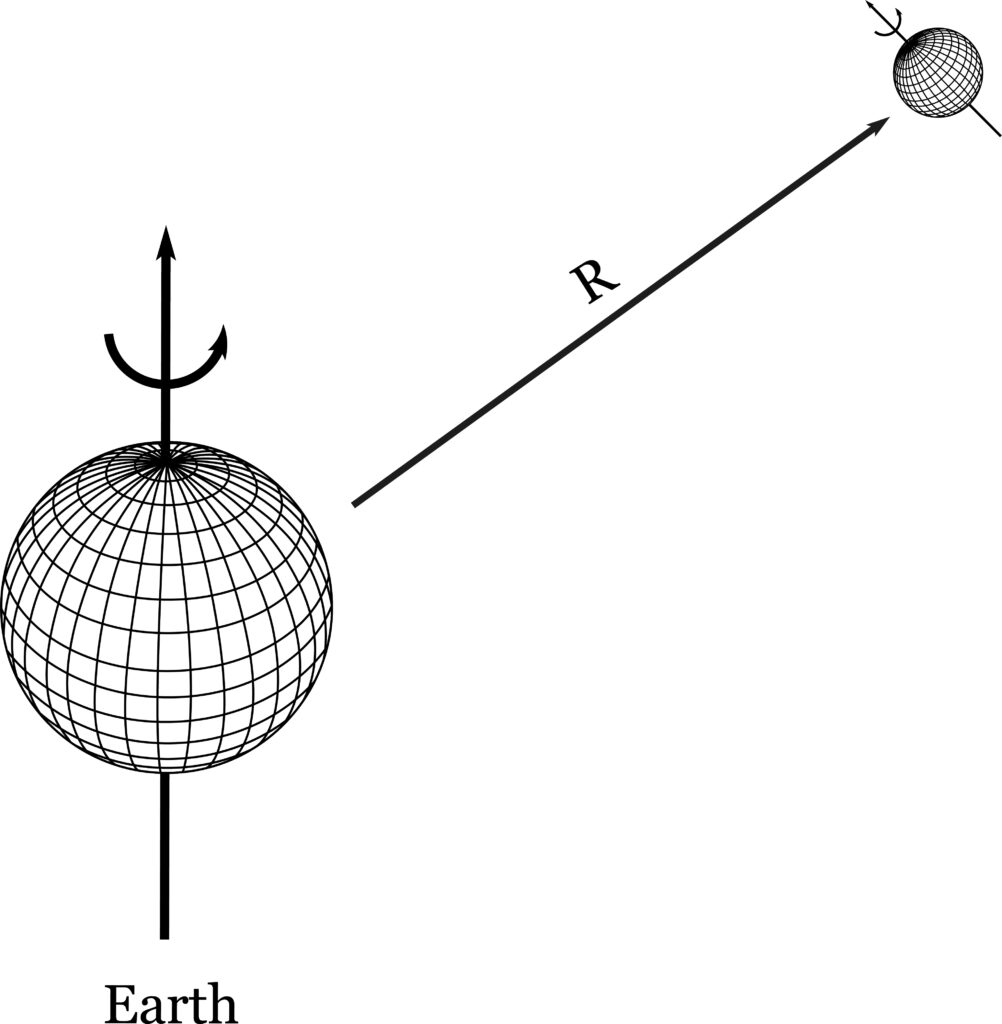
This deficiency, as well as that of scale, are taken care of in spherical coordinates, which we will now consider (fig. 27). Spherical coordinates, like Cartesian coordinates, comprise three mutually perpendicular axes. But in this case, the origin is assumed to coincide with the observer. Orientation is referred to this observer, and the object is seen as though on the inner surface of a hollow sphere. The distance of the object is given by the radius, R, of the hollow sphere, and the direction in which it lies and its shape are given by angular measurements of longitude and latitude.1 The latter measures correspond to the horizontal and vertical dimensions of a drawing, while the distance, or the radius, is equivalent to the scale of Cartesian coordinates. Orientation is taken care of because the observer himself provides the base with reference to which angles are measured.
It is obvious, therefore, that the spherical coordinate system is more complete, for it includes both scale and orientation. Furthermore, by the fact that the measurements of the shape of the object are in terms of angle instead of distance, we are reminded that the distances of Cartesian coordinates are not distances at all, but proportions. The drawing of the box tells us that it is twice as long as it is high, or the like; the drawing cannot give its actual size, except through the reference of scale. Hence it is not the dimensions of the object but their proportions that the drawing depicts.
There still remains an important point. Since Cartesian coordinates do not include scale and orientation, how are these aspects established?
Let us assume we are looking at an architect’s drawing of a house. How are scale and orientation established? The apparent size of the drawing varies as the eye of the observer moves toward or away from it, and there is a precise distance where the drawing may be held at which the building it depicts is the same apparent size as the actual building. As mentioned before, this distance would be such that the drawing would exactly cover the outline of the actual object (fig. 28).
The ratio of the two distances is the scale of the drawing.
Scale of drawing = drawing dimensions/actual dimensions
Similar considerations apply to orientation. Both the drawing and the building require the reference of a level or plumb bob which denote the horizontal and vertical directions of the actual world. For the observer, living and acting in this world, the horizontal and vertical directions are a prime consideration, indeed, a prime condition of his existence, for the mere act of standing requires continual muscular adjustments to maintain an upright position. This control is basic to being alive, so much so that the outward sign of death or illness is to fall down.
We conclude that the drawing or map in Cartesian coordinates, and, in fact, the Cartesian coordinate system itself, is included in and must be completed by a spherical coordinate system whose origin is the observer, and in which distance from this origin is the reference for scale. Orientation of the object is ultimately resolved by reference to the coordinates of this origin, which is the observer himself.
The relevance to science of the non-objective
At this point, the scientific reader is likely to object that such considerations are irrelevant to scientific objectivity, which is concerned only with such description of the object as would be common to all observers. Science, he points out, is careful to eliminate just that aspect of observation that we are reinstating by emphasis on the spherical coordinates of the observer. Apparent size and orientation are not objective realities and have no significance for scientific inquiry.
We could answer this criticism by pointing out that, since the conditions we are emphasizing are present in all scientific observations, they are as much a part of reality as are the objective determinations themselves, not because they concern the object but because they are an inevitable part of the act of observation. Support of the importance of the relation between observer and observed in a world scheme comes both from Heisenberg’s Uncertainty Principle and from the theory of relativity. The former calls attention to the inevitable energy exchange involved in observation of individual particles such as electrons, an exchange which makes complete predictability and, hence, objective determination impossible in theory as well as in fact. The latter calls attention to the impossibility of establishing simultaneity, and, hence, of the impossibility of identical world views.
Since science is based on observation, and observation involves dimensionalities which are not necessarily objective, we must give attention to just those aspects of the act of measurement which underlie or precede objectivity.
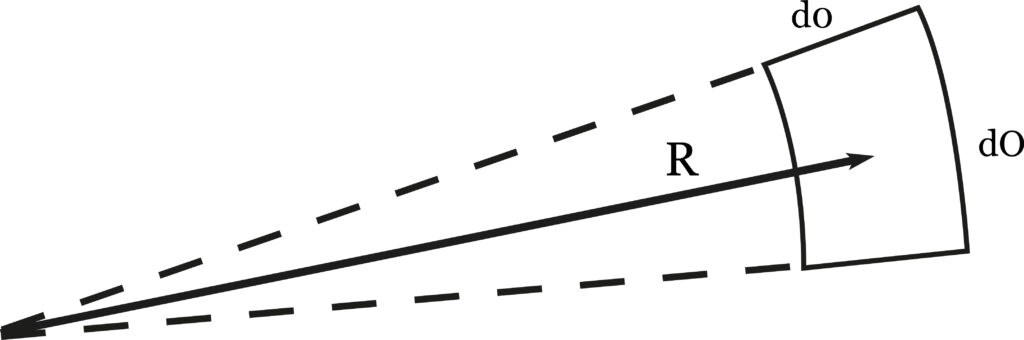
What does the spherical coordinate system teach in this regard? We may at once note that the R dimension is of an altogether different nature than the two angular dimensions dO and do (or the x and y of Cartesian coordinates).
In the first place, the two angular dimensions occur together, and are inseparable from one another. To speak simply, they are the dimensions of a surface. The radius R, which is the distance away of this surface, is a linear dimension. The surface dimension involves two numbers, or measurements; the linear dimension, only one.
In the second place, the dimensions that describe the surface may be read either way. Longitude may be measured east or west, latitude either north or south. In format terms, the numbers which measure a surface are positive or negative, that is to say, they are numbers associated with signs. In fact, in some applications, it is convenient to assign to the vertical axis (or latitude) what are called imaginary numbers. These, we will endeavor to show, are not so much numbers as signs, and designate directions perpendicular to those indicated by the plus or minus sign. In other words, the two-dimensional plane creates the necessity of four kinds of signs to describe direction.
Returning now to the linear dimension, the radius R, let us note that it is both empirically and logically prior to the two dimensions that measure position and shape on the interior surface of the sphere. We now assert that, in itself, R is without sign. We speak of an object as being two miles away, but it would make no sense to say that an object is minus two miles away. This might lead to our saying that R is only positive, but positive has meaning only when contrasted with negative; it is meaningless to speak of R as positive when it cannot be negative. Hence we say R is a signless number. This implies that this R dimension is one-way (like time). It could be objected that we can measure R either way, but the answer is that when we measure R “backwards,” we are measuring from the object, not from the origin.
It is very difficult to accept this notion (that R can be measured only one way) because we have become accustomed to viewing a linear dimension as one we can measure either way-we add and subtract distances on a ruler or sums in a bank account. But this measuring cannot be done until we have the two simultaneous dimensions of the surface as the matrix for our operations of transporting measuring rods and reading intervals of length by their coincidence with markings on the ruler. In other words, the linear dimension we measure in this way is part of the surface perpendicular to the line of view.
This may be seen when we “measure” R. To do so, the observer must shift his position and place himself at right angles to R, and view it as extending across his line of vision instead of along it. This implies he is no longer at the origin from which R was initially struck. We have taken a new viewpoint. In this way the linear R dimension eludes objectivity; for when we stand on one side to “measure” R (thereby making it objective), we create a new origin and a new R, which is not objective (fig. 30).
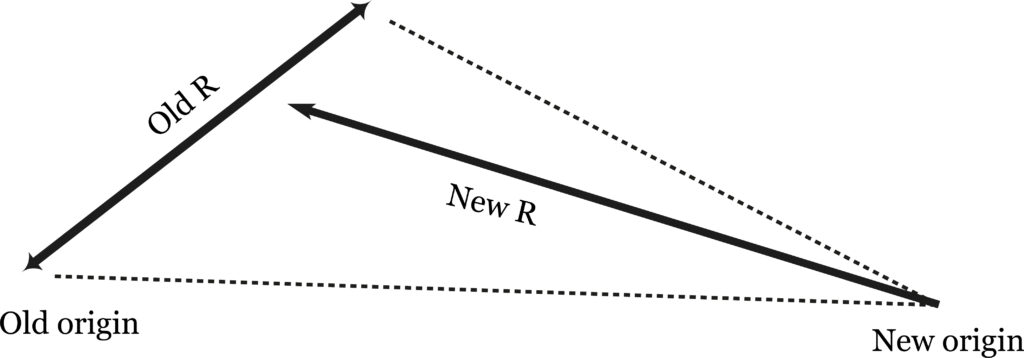
So there must always be a non-objective R in an objective observation. To avoid the limited connotations of the word “subjective,” we may call R projective. To reiterate our point, what is important for the question of dimensionality is that this one-dimensionality of R is prior to objective measure, and that it is a dimension without sign.
There is another aspect of the R dimension that, while it might seem to impose a loss of generality, so enriches its meaning that it should be mentioned. This is that the R dimension correlates with time. Time here is as it is experienced, and not that abstraction to which we refer when we measure time, in which case we have to “view” time from a vantage point outside of it, just as to measure R we have to view it from an origin that is separate from it. Further, the correlation of R with time does not exclude space. R is, rather, both time and space together before their separation by analysis. Thus, when we say something is four miles away, we might also say it is an hour’s walk away, recognizing that time and space are both involved. Here again, we can recognize that whereas measurement across our line of view is accomplished independently of time (we can estimate angular distances of remote objects instantaneously), radial distance, even when measured at the speed of light, requires time (a signal to the nearest star, for example, requires a time interval of ten years to go out and return).
We can now confirm an earlier statement. We said that R cannot be measured backwards. Suppose we extended R, say, by a signal to a distant star. At the speed of light this requires some five years. We now have the signal return; the time, unlike the distance, is not reduced as the signal returns; it continues to add, and when the signal reaches the starting point, the time elapsed is double what it was when it reached the object. The example gives reality to the notion of signless dimension. But we should not limit its application to time. There are a host of quantitative measures that are signless, viz., absolute temperature, mass, density, frequency, and so on, as well as “distance away.”
Finite and Infinite
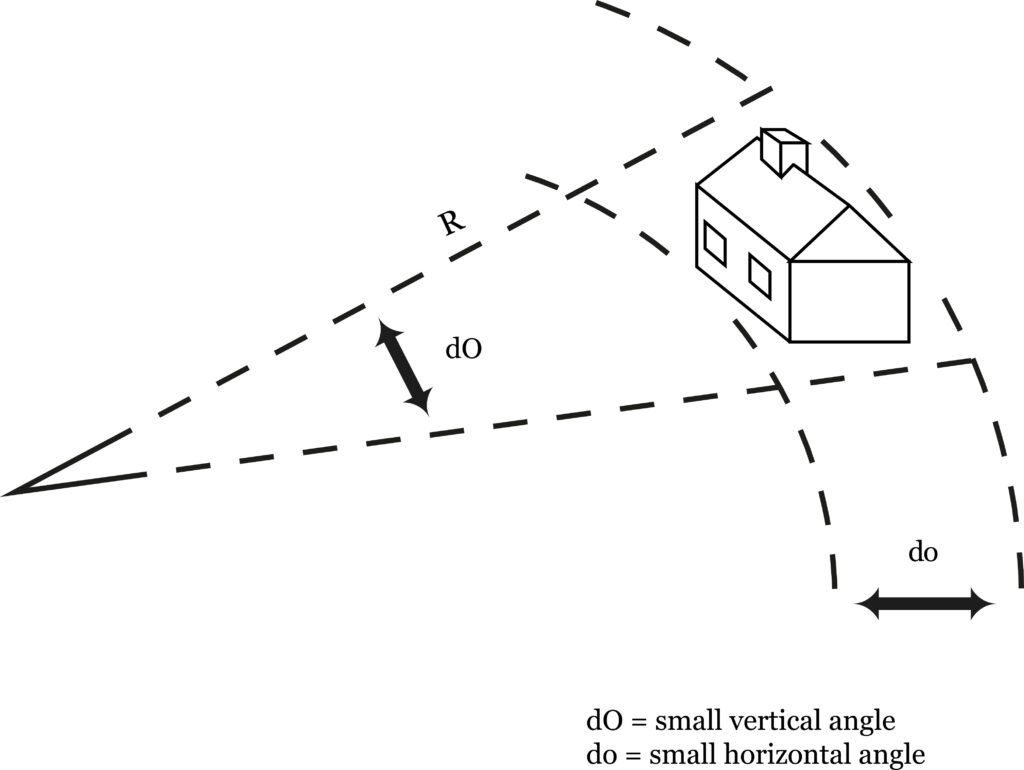
Dimensionality, then, is of at least two kinds: one-dimensionality, which applies to the measure of how far away something is, and corresponds to the radius in spherical coordinates, and two-dimensionality, which applies to the measure of shape or position, and corresponds to latitude and longitude. The former gives the scale, and is a measure of the “bigness” of an object; the latter is independent of scale, and yields the propqrtions and direction of an object. The former is in the “line of view” of the observer, and the latter is perpendicular to this line of view, a screen, as it were, intersecting the line of view (fig. 31).
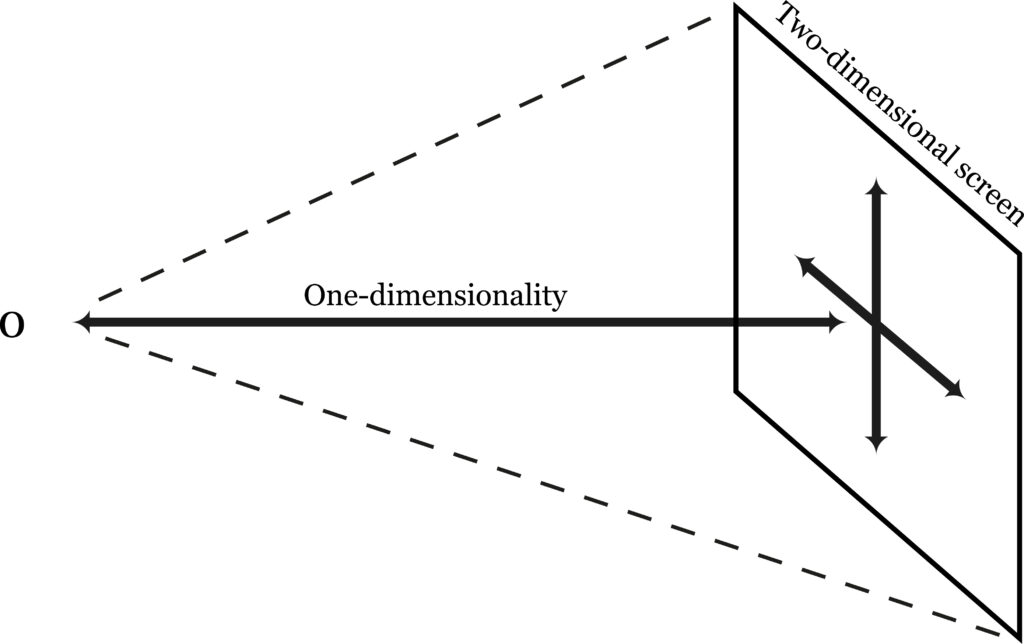
We may now note an interesting point: the R dimension (determined by the time required for light signals to reach the observer from the object), has no upper limit, and may extend indefinitely, whereas the two-dimensional screen has, for any fixed R, afinite extent. For, as we enlarge this screen, we see that, if R is to remain the same, it must curve around the observer (fig. 32).
The screen can become no larger than would be required to fill the entire field of view, and becomes the interior surface of a sphere, with the observer at the center. The measure of this field of view is in terms of angle; it is the maximum amount of rotation sideways and up and down, the maximum angle through which the observer can turn his eye or his telescope. This maximum angle is 27pi, or 360° in either direction. Hence the dimensionality of the screen which extends across the line of vision is quite different from the dimensionality of the “distance away,” the R dimension (fig. 33). Not only is it angular whereas R is measured in terms of length, but in its maximum extent it is finite, whereas R has no upper limit.
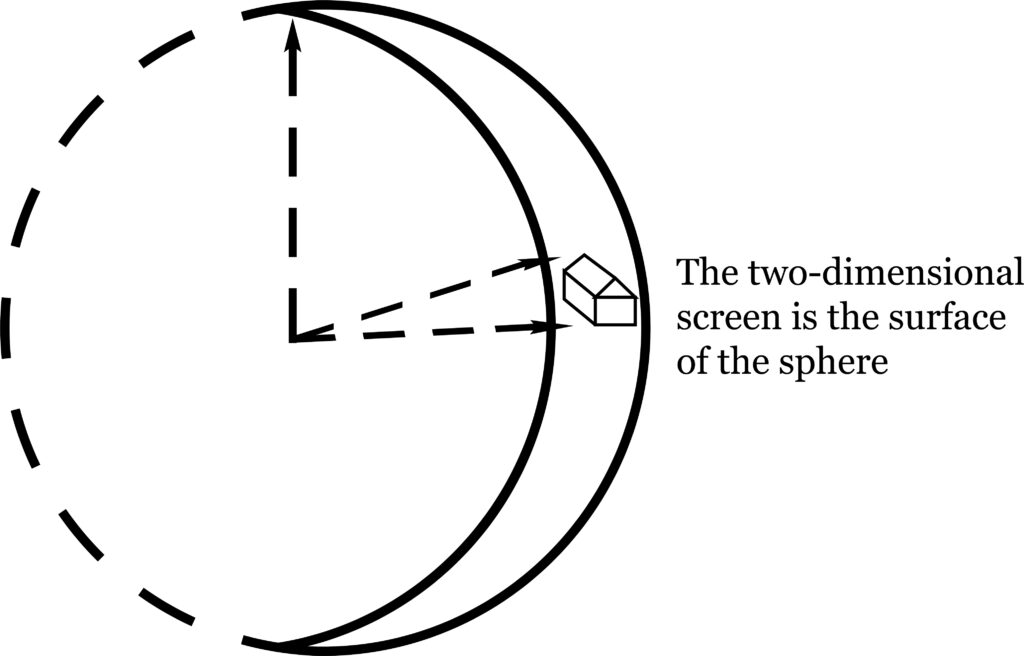
This is not to say that the interior of the sphere seen by the observer may not be as large as you please, but such size is contributed by the radius, and not by the angle.
Position and Rotation
We are ready for a further point: the distinction between the position of a body in space and its rotation around its own axis. This might appear to carry us into refinements only necessary to an astronomer, and without significance for the notion of dimension in general, but investigation will show that the concept of rotation is very important to and actually helps resolve the problem of dimension and extends its significance.
In a typical instance, an observer is situated on the earth and looks out at, say, a planet, itself rotating (fig. 34). The observer makes two sets of observations:
- The set that determines the position of the planet in terms of the latitude, longitude, and distance away with respect to the observer.
- The set that determines the rotation of the planet, which includes the direction of its axis, given in terms of two angles, one lateral and one vertical, and the number of rotations in a unit of time.
Note first that both of these determinations reiterate our distinction between the two-dimensionality of angle, and a one-dimensionality which, for position, is distance away, and for rotation, a number divided by time (e.g., revolutions per minute).
In the last analysis, all these determinations depend on time. This is evident if we recall that the observer is himself rotating, and determines the longitude of the planet he observes by the time at which it rises, sets, or passes the meridian (directly overhead).
Since this rotation of the observer is the basis for regulating and setting his clock, it is also basic to his measure of the planet’s period of rotation. Again, rotation establishes the direction of the equator and, hence, fixes the base for both the latitude of the planet’s position and its axis of rotation.
Finally, the distance away of the planet is measured by the time taken for a signal to reach it, and this time, in turn, is measured by the earth’s rotation. So we have all the parameters required to describe the planet’s motion depending on time, and, hence, on the observer’s rate of rotation.
This is not to say that these measures could not be determined by an observer on another planet independently of the earth’s rotation; what is implied is that this other observer, or any observer, would find himself in the same situation, all his observations stemming back to his own rotation.
We have seen the importance of rotation in establishing these measures, both because it is the basis for setting clocks and because the axis of rotation establishes latitude. We must therefore accord rotation the status of a dimension. As it is prior to the one-dimensional extension of the radius, we may call it a zero dimension, or zero-dimensionality. In addition to providing the basis for the other dimensions, we may here note that it establishes orientation, a factor, as noted earlier, not included within the Cartesian system. (To the extent that it occurs in Cartesian coordinates, it is accidental, a supernumerary factor which has to be supported by references outside the system.)
Since the zero-dimensionality of rotation is the basis for the dimensionalities of the line and the surface, we may correlate zero-dimensionality to the point, and thus complete the analogy which portrays one-dimensionality as a line, and two-dimensionality as a surface. But in doing so we must recognize that the point in this case is associated with a number, i.e., a frequency. Why, we might ask, does this numerical measure not make zero-dimensionality like the one dimension of scale, which also has one numerical measure? The tentative answer is that the rotation of zero-dimensionality is a “pure number,” devoid even of the property of extension, either in time or space, which characterizes one dimension. The point is devoid of extension, and we should keep in mind that, while we can call its number “frequency,” we have already correlated time with one-dimensionality, and to define zero-dimensionality as frequency or inverse time would be to invoke a circular definition. (Frequency is inverse time because it is a number divided by the time required for that many rotations.)
The ambiguity can be settled by making the number of zerodimensionality an undefined term, and hence fundamental. What we call time, and correlate with one-dimensionality, we can then define as the inverse of this undefined term. This is not a dodge, it is rather a matter of getting first things first. We must expect undefined terms, and it is proper that they should be the originating term in an ontological declension.
As we expect to clarify these issues in what follows, we can postpone this question for the present. We emphasize, however, that our study of dimension has indicated that at the root of the time and space measurement there is a number which counts rotation or frequency. Itself “dimensionless,” it is the origin of dimension. We call it zero-dimensionality.
Three-dimensionality
None of the dimensionalities discussed are appropriate for the “three-dimensional” world of physical objects, but we may adapt them to this purpose by saying that in the “three-dimensional” physical universe, the one- and two-dimensionalities of spherical coordinates are combined. I incline to the view that a different dimensionality is not required. Despite this assurance, one is habituated to thinking of the three dimensions of space as coexisting and objective, even though the act of measuring them always involves the procedures of spherical coordinates, requiring two kinds of measure: the one of scale (radius), and the other of form (latitude and longitude).
There may be some sense in which the dimensionality of physical objects is more than a combination of one- and two dimensionalities, but for the purpose of this analysis-which, as will be seen shortly, draws significance from the dimensions not measured as well as from the minimum number of dimensions that will suffice for measurement-it is not necessary to endow the dimensionality of physical objects with any properties which would not flow from the combination of one and two dimensions.
A further point about physical space (characterized by three-dimensionality or one- plus two-dimensionality) is that, as Kant said, the universe of physical objects is unique; there is but one physical world. On the other hand, every concept, every picture has its own space. There is no point in asking how far the tree in one picture is from the house in another2 because they have different space. The significance of this we now propose to discuss. It suggests that with the three dimensions of physical objects we reach an end to dimension.
Freedom vs. Constraint
The two-dimensional surface on which the position of a body is depicted in terms of latitude and longitude, and on which the shape of a body is described, may be at any distance. We look out the window and see the moon. It is 232,000 miles away. At the time of an eclipse it will just cover the sun, which is 400 times further away, and an equal number of times larger. There is no limit to the number of objects that could, like the moon, be between us and the sun, and just cover its image, provided they were smaller in the same proportions as they are nearer to the observer, and placed squarely in the line of view to the sun.
This is equivalent to saying that an object whose latitude and longitude are expressed, but whose distance is not, has a “degree of freedom” not possessed by an object for which the radius is given as well as the latitude and longitude. Similarly, if we specify distance away of an object but not its latitude and longitude, such an object has two degrees of freedom. It may be anywhere on the surface of a sphere whose radius is the specified distance. Further, if none of the three dimensions-longitude, latitude, and radius-are expressed, it has three degrees of freedom, or zero constraint. Thus we have:
- For zero- dimensionality, 3° of freedom, no constraint(s)
- For one- dimensionality, 2° of freedom, one constraint
- For two- dimensionality, 1° of freedom, two constraints
- For three- dimensionality, 0° of freedom, three constraints
We may now note two points:
- That dimensionalities are constraints.
- That the above relation between freedoms and con straints applies only to objects or to phenomena in the actual world.
This second point is necessary to meet the criticism of conventional mathematics (which insists that we may have any number of dimensions, with or without freedoms) that a dimensionality can be considered or devised that need not have this limitation. Here we would offer that such dimensionalities are fictitious. Not only is the observed physical world of objects three-dimensional and not four- or five- or six-dimensional, but even the postulated spaces-such as the flatland of two-dimensional creatures which was evoked to explain relativity in the 1920s-are fictitious. There are two-dimensional entities which “exist,” but such entities are possessed of one degree of freedom. For example, a circle is a two-dimensional entity, but because its scale cannot be specified except by reference to the physical world, neither the concept of a circle nor its description in a drawing go beyond stating its shape, and hence leave scale as a freedom. (Scale in a drawing requires experience in physical space as its reference.)
Similarly, there are one-dimensional “entities”-for example, velocity or momentum-but any actual velocity or momentum has direction, which requires two degrees of freedom to specify (two angular measures would be required). Other presumably one-dimensional “entities” such as temperature, population density, barometric pressure, etc., are associated with degrees of freedom: temperature with position in space, population with an area, barometric pressure with location in a volume.
But proof of the thesis involves questions of semantics. What is important is to recognize that postulations of “ndimensional” existence are either dealing in fictions or with actualities which have 3 – n freedoms usually overlooked or neglected.
II.
To the reader who may view an excursion into science as edious or demanding, let us explain that our ultimate goal is o apply this ontology to self and to achieve definitions of spects of consciousness. We have already noted the correpondence of the third level to concept, and hence to the easoning mind, and of the second to values (to which feelings nevitably attach). We can add that the first correlates with urpose and volition. Thus we have:
| Creation of an origin and direction of coordinate axes | = orientation, hence purpose. |
| Extension of a radius | = absolute magnitude, hence value. |
| Simultaneous measure of angle in two directions | = form, hence concept. |
| The combination of the foregoing to provide objective measurement. |
Thus it establishes the necessary orders in the process of generation and has significance for ontology (the “universal and necessary character of existence”). Ontology is general; it can be applied to many areas. In what follows we propose to show its pertinence to the basic entities of physics, an exercise which provides valuable feedback to refine the theory.
Correlation of dimensionalities to actual entities
We now take up the principal theme of our discussion, for which the consideration of dimension has been a preparation. This is that there is a correspondence between dimensionalities and the basic entities of physics. We have already hinted at such a correspondence with the suggestion that the world of concept is two-dimensional, and the world of scale, onedimensional, as well as in the question at the beginning of this essay, “Are there two worlds, the ideal world of mathematical relationship and a real world of actual objects?”
We may now generalize. We have seen that two dimensions are the basis for depicting form, and hence of objective definition and concept. We should recognize a similar inclusiveness in one dimension, and note that scale, in its dependence on an involvement with the object, is a special case of value. Thus value, like scale, is one-dimensional; in fact, it can only be indicated by a measure having a one-dimensional range. Otherwise, we could not say that one thing was more valuable than another. There is thus a correlation between dimensions and psychological functions (if we may so entitle the sense of value and the capacity to form concepts).
But the correspondence goes deeper, for when applied to the universe of physics, we can deduce the existence of entities which not only resemble the entities of physics, but predict their properties and behavior, and establish categorical distinctions between them.
The zero-dimensionality of photons
(Three Degrees of Freedom)
We may begin with electromagnetic radiation, whose ubiquitous presence is most familiar to us as visible light. Can one imagine a universe without light? The sun gone out, the stars extinguished? Hardly, for not only does the sun supply the energy for plant growth, and thence for all animal life, but without light we could observe nothing-perhaps not even think. And if this plea for the importance of light is insufficient, we can instance the generation of matter from photons, for a photon of appropriate energy can condense into a nuclear particle. And photons are also the end point in that ultimate destruction of matter which science is discovering in what is known as “gravitational collapse,” the final disappearance of matter which occurs when a star becomes so dense that its nuclear material collapses into a “singularity” (how effectively this word conveys its meaning without benefit of definition). Whatever this singularity is, it is not matter; it is something that can contain energy in less space than can matter, and this must be photons, which increase in energy as they decrease in size, or wavelength.
In short, the beginning of all things is light, by which we mean photons of all frequencies or wavelengths. (At a wavelength of 10-” centimeters a photon can produce a nuclear particle.)
Thus, in its smallness of dimension and in its possession of frequency, the photon conforms to the description of zerodimensionality, as a point with an associated frequency. Further, the photon conforms to a zero-dimensional entity in that it has three degrees of freedom, because its free passage in any direction involves two angular measures (two degrees of freedom), and its velocity of 186,000 miles per second constitutes a third degree of freedom, of distance, or extension. In answer to the response that this is a “limited velocity,” and hence a constraint, we must insist that the velocity of light is not a limiting velocity as is the “speed limit” on a highwayif the police were to chase a photon in a space ship, not only could they never overtake it, but however much power they exerted, and however closely they themselves approached the speed of light, they would still measure the speed of the photon away from them at 186,000 miles per second.
Thus our definition of zero-dimensionality deduces that the primordial entity of nature is point-like, is associated with frequency, and has three degrees of freedom.
It is now in order to make a turn about and obtain information from the photon to implement our definition of zerodimensionality. It will be recalled that we had to accept that the number associated with zero-dimensionality could only be distinguished from the number associated with one-dimensionality by the fact that it was a “pure number,” devoid of the property of extension. We can now draw on the known character of the photon to sharpen this distinction, as follows.
We know that the photon may be defined as a unit of action equal to Planck’s constant h. We also know that action has the measure formula ML/T, that is, it is energy (ML/T) times time (T), or momentum (ML/T) times length (L), or other combinations of these basic parameters of mass, length, and time. We now assert that such divisions of the photon are analytic, in a way, fictions; they are aspects of the totality, action, ways of dividing it into parts to which sense experience has access.
We earlier said that time could be defined as the inverse of the initial undefined term. This statement requires modification. The initial undefined term is action, but we can say that time is one of its components. Action is the product of time and energy. If we extract time (divide by time), we obtain energy!
The implication is twofold. In the first place, we can now say the initial photon, a zero-dimensional entity, has a constant as its measure (Action = Planck’s constant h). This avoids the difficulty of having to call it a pure number. We have traced the dimensions of cosmological genesis to a dimensionless constant.
In the second place, this cosmological goose egg, Planck’s constant, when it hatches out into one-dimensionality and produces time, also engenders energy, or mass and length. The same womb that produces number and dimension produces mass and energy. This conclusion is of great significance, for it demonstrates how “physicality” emerges from ideality, how physics unfolds from mathematics.
The one-dimensionality of nuclear particles
(Two Degrees of Freedom)
In terms of dimensions, the line is extension and the birth of time. In terms of the entities of physics, this extension manifests itself as nuclear particles, protons and electrons, whose rest mass makes temporal existence possible. This rest mass is the permanent investment that makes the physicality of the universe possible, for like “real estate” it has tangible reality. That is, a nuclear particle interacts with other particles without loss of its rest mass, whereas the photon is completely transformed in its interaction with matter. Even if the photon makes a partial expenditure of its energy, as in the photoelectric effect, what emerges from the encounter is not the same photon, but a new one.
The rest mass of the nuclear particle, by its permanence, contributes both substance and duration. We might say that it is this persistence that creates time, or that the creation of time requires permanence as a referrent. But time and substance are not enough; a third element is necessary. The need for a third element springs from the essential one-wayness of time. The notion of succession requires two things, plus an indicator of which comes first. This deduction is supported by reference to nuclear particles. As we were previously able to obtain information about zero-dimensionality from the photon, so we can obtain information from the proton and electron about linear one-dimensionality.
The third element is charge, and its asymmetrical association with mass (the positive proton has a mass 1,800 times that of the negative electron) establishes the basis for such other asymmetries as time direction, attraction and repulsion, etc., and accounts for the distinction between value and scale. We said previously that scale was a special case of value. We can now add meaning to this: the “desirability” factor in value (not present when, for example, we are talking about numerical “value”) has its ontological basis in the asymmetry of nuclear particles: the electron revolves around the proton, not the contrary.
To sum up, then, there is at this second level of generation an essential threeness, whether we call it time, motion, and change, or persistence, change, and interrelation. Nor is this richness only present in nuclear particles. Once alerted to it, we discover it in dimension, for the asymmetry of time is one of its essential and irreducible attributes; past and future are not interchangeable, logic to the contrary.
With this assurance (that the one dimension of time implies a threefold syndrome), we can go on to designate nuclear particles as entities with one dimension of constraint and two dimensions of freedom. Their constraint is persistence in time, but for the purpose of this analysis, the nuclear particle results when a portion of the original energy of the photon is precipitated into rest mass. This amount of energy (I BEV), formerly unpredictable, becomes exact and known; the remainder continues as the product of two uncertainties, that of position and that of momentum (L x ML/T = ML2/T).
Thus, a nuclear particle is a fixed amount of energy (in the form of rest mass) of uncertain position and momentum. Admittedly, this view of a nuclear particle omits Heisenberg’s observer who “cannot determine its position without changing its momentum, and cannot determine its momentum without a time interval during which its position changes.” The view here taken draws upon mathematical usage in which the specification of one of three dimensions leaves the other two unspecified, or “free.” The present view goes further only in that it invests such a mathematical entity with real existence, citing a nuclear particle as a linear entity.
The two-dimensionality of atoms
(One Degree of Freedom)
This brings us to atoms, which interchange the roles that constraint and freedom play for nuclear particles. Atoms at absolute zero temperature are without self movement; their position can be fixed and determined, but their energy cannot! An atom, even at absolute zero, is free to emit or absorb energy (in the form of photons). Thus, we can say that an atom possesses two-dimensional constraint and one-dimensional freedom.
We may also view the atom as having a two-dimensional nature, in that its orbital electrons establish a plane of symmetry, a two-dimensional matrix in which the form principle operates to create the precisely determined electron configurations known as rings or shells (according to the Pauli Exclusion Principle). It is these configurations which dictate the chemical and other properties of the over 100 kinds of atoms.
Note the important philosophical principle that properties are constraints. The more qualifying adjectives and phrases are added to the description of an entity, the narrower (more constrained) it is. “A house” could apply to almost any habitation, “a six-room house” is a more limited category. The atom, being the bearer of “properties,” is more constrained than the nuclear particle, whose properties are limited only to its mass and charge. So we see the dimensional concept applies metaphorically as well as literally; the dimensional constraints of an atom correlate with its possession of definite properties. In fact, it is two-dimensional constraint that makes form possible. There can be no “form” in one dimension. Similarly, substance has no “properties” save that of substantiality.
The three-dimensionality of molecules and molar matter
(Zero Degrees of Freedom)
The fourth category of three-dimensional constraint correlates with molecules and molar matter. While it is true that molecules have an inherent motion at ordinary temperatures even when locked in crystals, and are only completely inert at absolute zero, this random motion is not an inherent motion, it is imparted by impact with other molecules which are agitated by temperature.
Even this motion due to temperature disappears for aggregates of molecules, the so-called molar objects, which are the physical objects we see and touch, the world of matter which is subject to the laws of determinism, and whose behavior was judged by nineteenth-century science to be typical of all objects, including the ultimate particles like atoms and electrons.
The view that we are here expounding-that determinism is a special case-is that of contemporary science, though it must be admitted that science today does not give a positive meaning to indeterminacy.
To a great extent, this lack of emphasis is due to science’s ingrained respect for law. This “respect” is essentially aesthetic; the rational mind has difficulty accepting indeterminacy, which cannot be distinguished from chance or accident. As Einstein said, appropos of his reluctance to accept the quantum theory, “God does not play dice with the universe.”
This remark of Einstein’s bears some scrutiny. It is not, as would first appear, a religious statement. The God of the Old Testament, for example, did indeed take a chance in giving man free will. Nor can we allow the notion that chance and free will are essentially different, since to an observer there is no way to distinguish between them. If Einstein was sincere, we must interpret his sincerity as naive, like that of the soldier who believes that he has God on his side. The side, in this case, is that of the rationalist who cannot, or does not wish to, conceive that there is anything in the universe not subject to law.
But here, with molar matter, the factor of chance is minimal; the planets do obey exact laws, and inert objects like paperweights do not exhibit self-caused or spontaneous action. The progressive diminution of freedom which characterized photons, electrons, and atoms is in molar matter complete; constraint has taken over entirely. We have reached the end of the spectrum that runs from complete freedom to complete restraint.
Higher Dimensions
Let us recapitulate the main points so far. By reference to the actual operations necessary to measure objects in space, we first established that dimensions involve much more than “pure” number. They exhibit a difference in kind which provides the basis not only for different aspects of reality–viz., its scale or “value” aspect as well as its conceptual or measure aspect-but different orders of “reality,” viz., nuclear particles, atoms, etc.
Going further, we discern that each order, or aspect of “reality,” is characterized by constraint and freedom in varying proportion, but of constant sum, being such that the total dimensionality is always three. The significance of this is that it establishes, albeit empirically, that there are no more than three dimensions-or four dimensionalities, for we must include the case where there are zero dimensions (no constraint). This would appear to indicate the impossibility of higher dimensions-four, five, and six dimensions.
Such higher dimensions have often been hypothesized. It was argued that just as a plane moved perpendicularly to itself produces a volume, so a volume moved at right angles to itself will produce a four-dimensional figure.
The implication was that because we can know both a plane and a volume, there is no reason to stop there; there must be higher dimensional figures. In the light of our present analysis, however, a plane is not so much a two-dimensional figure as it is the specification of two out of three possible dimensions, and hence can be moved to create a volume; whereas a volume, in which three dimensions are specified, has no further freedom into which to move, so it does not follow that four dimensions are possible.
We may, of course, take the position that dimensions beyond the three physical ones are of a different sort, i.e., that they are not accessible to the physical senses. This cuts us off from experimental verification, and exposes us to the same criticism that has been leveled at the ancients, whose doctrine of epicycles to explain the motion of the planets created a new hypothecation for each new factor.
However, we do have sanction from nature for a different kind of dimensionality. The formula for the interval between two events (interval is distance plus time) is expressed in Pythagorean fashion as the square root of the sum of the squares: I = (the square root of) dx2 + dy2 + dz2 – dt2.
In this expression, x, y, and z are the dimensions of space, and t is time. Unlike the x, y, and z dimensions, time has a negative coefficient. Since the negative sign is associated with time squared, time itself must have the square root of negative unity as its coefficient. This, of course, is i, the imaginary. It is essentially different from space.
In space I can measure a step forward, a step to the right, and a step up; each direction is perpendicular to the one before. But if I am to take another “step” in a direction perpendicular to all three, it cannot be spacelike. It has to be a different time (later or earlier).
Eddington, in New Pathways in Science, makes this categorical distinction between time and space quite clear. He does so, however, in connection with his E-operators, which are beyond the scope of the present article.
Thus the distinction between space and time is already foretold in the structure of the set of E-operators. Space can have only three dimensions, because no more than three operators fulfil the necessary relationship of perpendicular displacement. A fourth displacement can be added, but it has a character essentially different from a space displacement.3
For present purposes, the E-operators by which Eddington arrived at this conclusion are not essential. The same categorical distinction between space and time is implicit in the formula for interval, indeed, in the commonsense distinction between time and space.
Common sense, then, recognizes the distinction. How does mathematics recognize it? To answer this we have only to note how the imaginary coefficient was created. In fact, it would be better to say we should note how the imaginary coefficient forced itself on the attention of mathematicians. For it only emerged when mathematical formalism took on a life of its own and dictated the necessity of entities to which no physical correlates could at first be found.
For those not familiar with the subject, a brief historical account is in order. In order to solve problems (of an algebraic sort), it was found possible to set up an equation such as: x2 = b (x times itself = B What is b?).
The solution, x = plus or minus the square root of b is straightforward (for example, x2 = 4, hence, x = ± 2), but there arose situations in which x2 was equal to a negative quantity: x2 = -1.
The solution — square root of -1 — had no physical correlate, and was for some time set aside as imaginary, by which word it was judged to be “false,” or “illusory.”
However, Gauss and others found a representation for the imaginary as a “direction.” Thus, if plus and minus are represented as opposite extremes of a line:
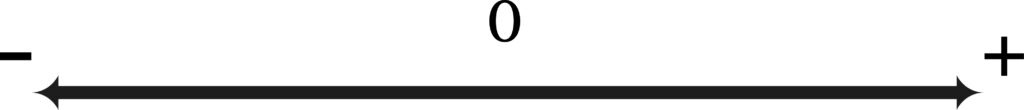
We can think of the square root of minus as a 90° perpendicular to this line.
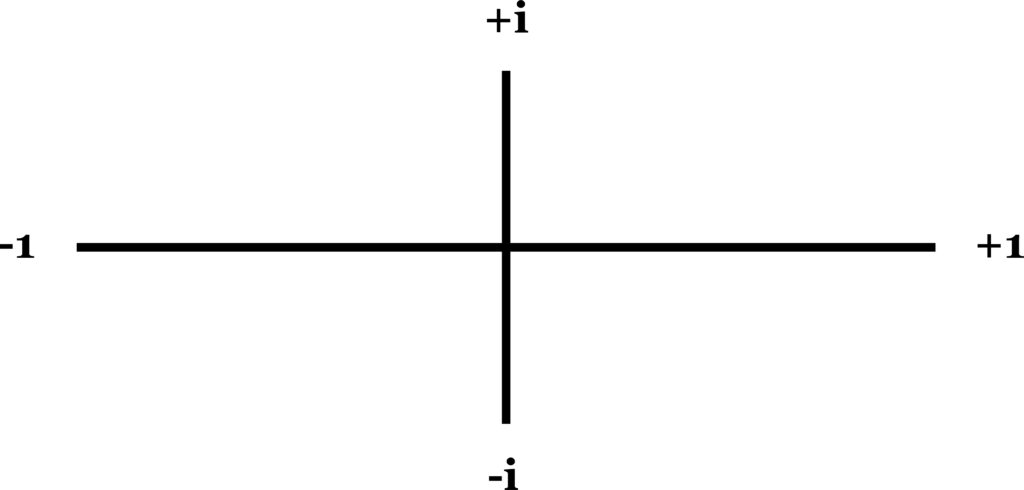
This new idea emphasizes that the oppositeness of plus and minus, like the oppositeness of North and South, is but a partial account of a more extensive domain of direction, and that what had been dubbed imaginary is actually the mathematical counterpart of spatial direction, which is not just North and South, but East and West as well.
This expansion of mathematical usage has been tremendously fruitful, and the imaginaries now have a usefulness equal to that of their counterpart, the real numbers.
The lesson this teaches can be applied to the question of the origin of dimension. As we said before, the usual concept of dimension is additive. First we have the point with no dimension, then the line with one dimension, the plane with two, and the volume with three. But where have these added dimensions come from? They seem, like rabbits out of a hat, to be materializing out of nowhere. Surely, if we are sincere ontologists, we must give a better account than this. (Even if we abandon the deductive account of dimension and draw on the physical universe, then we must take the position outlined in the beginning of our essay and view dimensions as existing in the first place as freedoms, or blanks to be filled in. Such a course limits us to three dimensions and no more.)
However, if we recall that the operation of taking the square root of negation produced an independent dimension perpendicular to the other “diametrical” opposition of plus and minus, we are alerted to the fact that, at least in this case, a dimension is created “out of nothing” by the operation of taking the square root.
This leads to a further step. How did the dimension of oppositeness (plus and minus) emerge? By taking the square root of unity! In other words, if we find the square root of one we obtain two opposite values, +1 and -1, for either of these multiplied by itself produces unity.
In other words, we obtain one dimension (the range of values between plus and minus) by extracting from unity its square roots. The extraction of roots unfolds the dimension. We obtain the two dimensions of a plane by a second application of extracting a square root, which is the fourth root of the original unity. Note that the first extraction of the square roots of unity is disguised by the convention of plus and minus, which does not so much create a new kind of number as it does a dimensionality of existence for the operation of number.
The second application similarly creates a two-dimensionality, but here the convention is to refer to the + i and – i as square roots, whereas ( + ) and ( – ) do not have this other name. We can therefore trace the origin of dimension to successive extractions of roots of unity, the two applications thus far producing two dimensions whose typical equation is the circle.
A third application of a square root generates a quartic. A typical equation is:
(x2 + y2) / y2 = 1
This equation can represent a circle rotated 180° about a point on its circumference. By continued rotation such a circle produces a torus with an infinitely small hole, and is presumably a more general figure than the more commonly recognized sphere or cylinder, either of which would be created by moving the circle perpendicular to itself.
Here I would refer my reader to a very interesting paper by Dr. Charles Musès, “Time, Dimensionality and Experience.”4 Using algebraic methods, Musès shows that dimensionalities can be coded as the degrees of certain characteristic equations. In carrying out his program by successive increase in the degree of his equations, he performs the equivalent of what we have shown is accomplished by extracting successive roots of unity. Both methods produce the same results, but for the present ontological survey, derivation from unity by the extraction of roots has an advantage, because it stresses the dimensionless origin of dimension. It is interesting that p has the property p2 = 0, p (not =) 0, which means that the origin is on the surface.
Musès shows the generation of dimensionalities of a higher order, and gives characteristic equations of sextic and octic degrees. What is most interesting, in the present context, is that as the degree of these equations (referring to higher kinds of number or dimensionalities) increases, the successive laws of algebra break down. First the commutative law, then the associative and distributive laws, until finally the field forms become multiform. In other words, in sufficiently higher dimensionalities, results are increasingly indeterminate. A given set of conditions will not produce a predictable result. This I would interpret as equivalent to saying that dimensionalities beyond the third see the reintroduction of freedom.
With this encouragement from Musès, let us pursue the implications of the scheme that we have so far laid down. This involves an extrapolation as to what must be beyond the three constraints which apply to physical objects. To perform this extrapolation, we have need of another principle not heretofore noted.
The cumulativeness of dimension
This principle is that, as we move from one dimension to the next, we retain what has gone before. Each dimension builds on the one before it. This is easy to see in the case of three dimensions, for in making measurements of a real object, we have access both to the two-dimensional concept, or shape, and to one-dimensional extension, or scale. We say the box is 10″ x 4″ x 2″, which describes its proportions and assumes the inch to be known. Only when we have to deal with unfamiliar units such as the cubits which measured Noah’s ark are we made aware that this normally taken for granted aspect of measure requires a separate determination. So the dimensionality which describes form has dimensionality which describes scale to back it up. The latter, in turn, draws on the point of origin for its meaningfulness, not only in that we must start the extension from a point, but in that we must be able to swing this extension about in whatever direction is required. This i the angular freedom with which a point is endowed, if it is to be the origin for observations. A telescope that could not be swung about would have a very limited usefulness. So dimensions are cumulative. This is clear from an inspection of the expression for distance in spherical coordinates. Note that:
- ds2 = dR2(dO)2 + R2sin2Odo2
- R = radius
- O = longitude
- o = latitude
The first term on the right of the equal sign includes R only, the second includes R and 0, and the third includes R, 0, and o. Each successive term includes the ones before. So we can expect of higher dimensionalities that they must include threedimensionality.
This inclusiveness has philosophical significance by reason of the integrity with which it endows higher dimensions. Were higher dimensions just added on, they would not contribute the “organic” properties we will now consider.
Higher Dimensional Objects
Coming now to the higher dimensions, we may expect, in accordance with the cumulative principle above, that higher dimensions must include lower dimensions. We have correlated the simpler or lower dimensionalities to the orders of entities recognized by physics:
| zero-dimensional | photons | 3° of freedom |
| one-dimensional | nuclear particles | 2° of freedom |
| two-dimensional | atoms | l° of freedom |
| three-dimensional | molecules and molar matter | 0° of freedom |
Can we extend this correlation to entities of a more complex nature than molecules? A hint comes from the fact that Musès finds that for the next higher dimensionality after p, entropy is negative.
Now it so happens that there are physical objects for which entropy is negative, for example, seeds. If we regard a seed, or, indeed, any living cell as a higher-dimensional object, we can suppose that the extra dimensionality it involves is somehow interior to it. Externally, it resembles any three-dimensional object; but unlike an inert object, it contains an internal organization which can store or expend energy.
How may we designate such an attribute in its simplest terms? The answer is to equate this capacity of the seed with power, for power is the technical term for the capacity to convert energy. We may thus view a seed, or, more correctly, the plant cell, as endowed with an extra intemal dimension, a power not possessed by the lifeless object.
Biologists have long sought for criteria to distinguish the living from the non-living. Is it growth? Reproduction? Sensitivity? Photosynthesis? If growth, then we would have to include polymer chemicals. If self-reproduction, we should include chemicals-notably the virus (which by other criteria is a kind of molecule rather than a life form). If sensitivity, then we must include metals, whose sensitivity to fatigue and poisons was specifically studied years ago by Bose,5 and is now generally recognized. If photosynthesis, then the fungi, which are classed as plants, would not qualify … and so it goes. It is difficult to find a criterion to separate the living from the non-living.
The true distinction between life and inert matter is that life-and we here mean vegetable life-moves against the current of entropy; it locally violates the second law of thermodynamics. This law states that any given distribution of states, such as hot and cold, ordered and disordered, tends to average out. A glass of cold water, left in a room of usual temperature, gets warmer; a glass of hot water gets colder. Stones roll down mountains and fill valleys. The sheets of a manuscript, when scattered by the wind, lose their ordered position; cards, when shuffled, attain more random distribution. All non-uniformity eventually evens out, becomes more average.
Plants, on the other hand, manage to store energy within their own confines. This, of course, is a local phenomenon. The plant does not create this energy, it draws it from sunlight and stores it as starch and sugar. So the plant’s activity does not affect the general situation; it is still true that the outpouring energy of the sun is wasting away; the second law of thermodynamics still applies in the larger framework. But locally, there is negative entropy; for as the plant grows, it stores more energy than it expends.
The plant uses this energy for its own metabolism and growth; without it there could be no metabolism, no growth. We can also view this storage of energy as storage of order. In fact, it is because the energy is stored as order that it is available as fuel to propel the life process, the metabolism which we could call manufacture.
Thus, the more correct statement of the law of entropy is that order tends to revert to disorder. Energy itself neither decreases nor increases, but the availability of energy decreases. In other words, order is available energy.
What the plant does, then, is to make energy available, to draw on the energy of sunlight and store it as order in starch molecules. It also expends this energy. This is important because, without this ability, the plant would merely store energy; this would replace one kind of determinism with another. It would have no “freedom.” The plant has the power to store or expend, and thus has a kind of freedom which exempts it to some extent from determinism. It enables it to grow and to reproduce.
Reverting now to the dimensionalities we discussed at the beginning, it will be recalled that the first constraint was to give a fixed value to R, which is extension. The capacity of the plant for unlimited growth, which is not just its own growth, but its self-multiplication into seeds which themselves grow, may therefore be interpreted as a kind of inversion of this original constraint. The plant has the power to increase its extension: it inverts the initial constraint and makes it a power. This is not the same as dropping the constraint, as would occur if a nuclear particle reverted to a photon, or a forest burned up and converted to radiant heat. The constraints of the earlier levels are retained, the plant or the cell accepts the limitations of matter and operates with them to grow into something millions of times its original size. In short, it escapes the limitations of determinism.
Of course, the concept of the plant as a higher-dimensional entity does not completely account for how the plant is able to move against entropy, but it does give formal recognition to negative entropy as a principle, and thus provides scientific status for what ordinarily has to be regarded as an exception to scientific law, an accidental or fortuitous emergence.
The problem of plant growth has always been a mystery, and, since science has no place for mystery, there has resulted a sort of internecine war between the mechanists and the vitalists about the explanation of life. The mechanists, clinging to their faith in mechanical law and insisting that life is “merely” chemistry, shove the issue under the carpet and do a disservice to science by failing to recognize that the existence of a problem that transcends available techniques should inspire better technique. The vitalists are equally at fault for obvious reasons, for to hypothecate a mystique which cannot be solved is to retreat from the challenge that motivates scientific progress.
This struggle between vitalism and mechanism is futile, because both parties fall short of the mark. Their adherence to Igpolicies” is a failure to adapt to a new challenge. (The word “adapt” has the same shortcoming here that it has in evolution-what is required is a creative thrust which penetrates more deeply into meaning.)
It is here that Musès’ inquiry has such value. For to discover in mathematics itself, or, rather, in implications which spring from the same foundations that have produced calculus, quadratic equations, and tensor analysis, a new and different mathematics, which deductively anticipates what has heretofore had to be classed as a mystery, is precisely what is needed for the growth of science.
It would be very gratifying if we could go further and anticipate more of the character of life from other implications of the mathematics of higher dimensionalities. What does the breakdown of the basic laws of algebra-the commutative law, the associative law, and the distributive law-mean in terms of life or other possible manifestations of nature?
Recognizing that there are several dimensionalities beyond that in which negative entropy first emerges, and that there are animal, and possibly higher orders beyond vegetation (or organization at the cellular level), is it possible that the higher dimensionalities correlate to the higher orders of entity?
Such speculations, could they be confirmed, would indeed close the gap between the two worlds-the ideal world of mathematical relationship, and the real world of actual objects (to which we can now add living entities).
Supplementary note
I believe that the real function of science today is the exploration of the living spirit of man. We are witnessing a revival of interest in psychic phenomena, ESP, dreams, telepathy, clairvoyance, altered states of consciousness, and even immortality and other manifestations not within the established disciplines of science.
What is lacking is obviously not proof of psychic phenomena. Rather, it is a theory capable of structuring and integrating the facts. Here we must recognize that, as Kuhn points out in The Structure of Scientific Revolutions, a scientific theory is never displaced by facts, it can only be displaced by another theory.
It has been assumed that these phenomena are outside the realm of physical theory. Sporadic efforts to invoke scientific procedures for investigating them (e.g., screening for telepathy) have been without issue. I believe it is time for some very careful rethinking, however, for it appears that the discoveries of modern science actually confirm mental aspects at the most basic levels of the physical universe. To show what I mean, I should first clarify the distinction between the physical and mental aspects of a situation.
When the message “come home” is sent by telegram, what actually happens is the transmission of electrical impulses along a wire. The electrical impulses, per se, have nothing to do with meaning. They must be translated into words by the telegraph operator, and finally into meaning by the recipient of the message. While the electrical impulses obey the laws of matter and occur in space and time, the recognition of the meaning of the message “come home” is not the kind of spacetime occurrence that science deals with. The faculty of recognition is quite different from the means used in the transmission of messages. Mind and matter are separate and distinct aspects.
While science purports to deal only with matter, I believe that quantum physics has been affirming what is at least an equivalent of mind in the concept of the quantum of action. In science, action is the product of energy and time. It occurs in discrete units (quanta) which cannot be further subdivided, and are the fundamental building blocks of the physical universe. One of its forms is the photon, or pulse of light.
I believe that events at this fundamental level of the physical universe can provide us with a language for dealing with the mental aspects of a situation, such as the fact that recognition occurs outside of time. While its antecedents take place in time, recognition itself is instantaneous. Similarly, time does not exist for the photon, since, according to relativity, clocks stop at the speed of light. The effect of the photon (i.e., altering the state of an atom) and the act of recognition are both quantized-the former by definition, and the latter in that you cannot somebody 1½ times. But, most significantly to this discussion, both are events in which some non-material entity alters the state of the recipient. (The photon is non-material because it has no rest mass.)
From the point of view of developing a science of ESP that is, a science in which something immaterial has primary status-these discoveries of quantum physics have great significance, in that they establish a scientific precedent for the existence of non-material influence, opening the door for the acceptance of a more extended range of phenomena.
However, the successes of quantum physics have depended upon mathematics to reach what is not available to the physical senses. I believe that the science of the mind can be developed only by the use of more advanced mathematical equipment. This is what first, attracted my interest to Dr. Charles Musès’ hypernumber theory.
For many years I have speculated that the imaginary numbers have some correspondence with the non-physical. Consequently, I was intrigued when I read Dr. Musès’ paper on higher numbers,6 which extends the imaginary to hypernumber, and shows that there are a number of dimensionalities beyond those by which we measure physical objects.
My conviction of the importance of Musès’ mathematical discoveries stems in part from the correspondence I have found between his dimensionalities and what I call the levels of process. My theory maintains that process must, by ontological necessity, involve sequential stages, each one building on the one before. The first step is aim or purpose. The succeeding steps see the initial aim, which is potential only, investing first in material, then in form, then in both together to produce what we call the physical world (particular objects or events). This is the world of determinism or law which classical science has long recognized.
The physical world constitutes a basis or foundation which is then “used” by process to create organisms (plants), living entities which employ physical law to grow and reproduce. This state of process is in my system the fifth, and I was struck by the fact that Musès’ fifth dimensionality was described as having negative entropy. Since negative entropy is the distinguishing characteristic of plant life, I was moved to look for further correspondences.
I found several–more than enough to convince me that, in quite different ways, we were both uncovering a basic structure in the universe. While these correspondences cannot all be described here, I will mention one.
This is the correspondence between what I call “freedoms” and what he describes as breakdowns of the three laws of ordinary arithmetic. Musès states that first the law of commutation breaks down, and indicates that in yet higher number realms the laws of association and of distribution break down, too.
For my own part, I have shown that my higher states “win back” first two, and then three “degrees of freedom.” It is significant to show a correlation between these stages and the successive breakdowns of the laws of ordinary arithmetic.
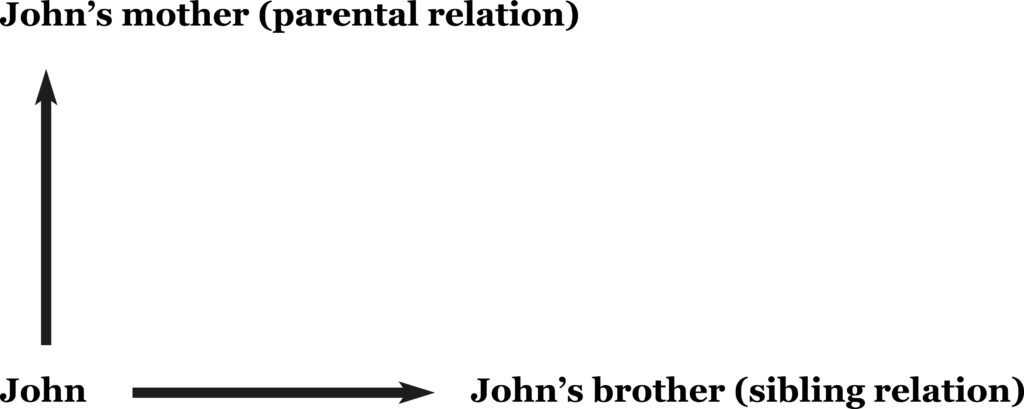
This I have recently succeeded in doing. The sixth state in my system is characterized by mobility, typical of animals, which exhibit voluntary motion (contrasting with the relatively “one-dimensional” freedom of plant growth). How to correlate this with the breakdown of the law of association? To do this, find an interpretation of a, b, and c for which (ab)c (not=) a(bc).
- Let a = brother
- Let b = John
- Let c = mother
Then (ab)c = the (brother of John)’s mother = John’s mother, whereas a(bc) = the brother of (John’s mother) = John’s uncle. What is it about this example that is responsible for the breakdown of the law (ab)c = a(bc)?
It is obvious that we are dealing with two kinds of relationship, parental and fraternal. These are two dimensions of relationship, the vertical relationship of parentage and the horizontal relationship of siblings. Hence, where two-dimensional choice (minimally necessary for true mobility) is involved, the law of association breaks down.
The breakdown of the law of distribution correlates with my seventh state of process. In my system, this stage is subject to but one law, the law of hierarchy. How does this correlate with the breakdown of the law of distribution?
Choose an interpretation of a, b, and c which will cause the law of distribution to break down.
Let:
- a = commander of
- b = company b
- c = company c
Then ab + ac means the commander of company b plus the commander of company c. But a(b + c), the commander of companies b and c together, is an officer superior to the captains of b and c individually–a colonel, at least–and two captains do not equal a colonel. This is the very essence of hierarchy.
I admit these are analogies. They are not what is customarily sufficient in mathematical proof. They do, however, have the merit of revealing the correlation between two distinct approaches-my theory of process and Musès’ theory of dimensionality. I offer them in the hope that the non-mathematical reader may be aided in grasping sometimes unfamiliar conceptual levels in hypernumber theory.
I see in the breakdown of the laws of ordinary arithmetic in Musès’ higher number spaces or dimensionalities a correspondence with the breakdown of physical laws in the realm of parapsychological phenomena, and I believe that his ideas may help in formulating theories covering these phenomena.
Footnotes
1More correctly, right ascension and declination, but longitude and latitude are the more familiar terms.
2See William E. Hocking, The Meaning of Immortality in Human Experience (1957), ed. (Westport, Conn.: Greenwood Press, 1973), pp. 26-28.
3Sir Arthur Eddington, New Pathways in Science (1935), Ann Arbor Paperback ed. (Ann Arbor: University of Michigan Press, 1959), p. 276.
4Annals of the New York Academy of Sciences 138 (1967): 646-60. The above equation is Musès’ p-field and represents two circles of half-unit radius tangent at the origin. The torus with an infinitely small hole is Musès’ circular umbilicoid, given by (X2 + y2 + Z2)2/y2 = 1.
5Sir Jagadis Chandra Bose, Response in the Living and Non-Living (London: Longmans, Green, 1910).
6Annals of the New York Academy of Sciences (1967). See also the same author’s “Hypernumbers 11: Further Concepts and Computational Applications,” Applied Mathematics and Computations 4 (1978): 45, and “Explorations in Mathematics,” Impact 27 (1977): 66.
©1980 Anodos Foundation









